In the coming weekend, one of the most important watches of this auction season will go under the hammer at Sotheby’s Breguet’s 250th anniversary thematic sale November 9 – Breguet no. 1890, a pocket watch with tourbillon and natural escapement made by the firm by Breguet while Abraham-Louis Breguet himself still helmed the company.

The gilt dial with a regulator-style layout might seem familiar – the recent Classique 7225 reproduces this dial design. In fact, Breguet no. 1890 isn’t the only watch in this style; it belongs to a series of pocket watches all equipped with a four-minute tourbillon and échappement naturel from the early 19th century that were among the finest watches of the time.

Breguet built just eight four-minute tourbillons with natural escapement, all of which thankfully survive, and only three with gold dials. King George III ordered the most famous example – almost identical to this watch – during the Napoleonic wars. For context, that would be like Churchhill (who owned a Breguet himself) ordering an A. Lange & Söhne watch during the Second World War. As such, it was signed Recordon, Breguet’s London agent, to disguise its French origins.

Whirling About Regulator

Almost 225 years ago, the French Ministry of the Interior granted A.-L. Breguet a patent for his most famous creation, the tourbillon – a clever exercise in lateral thinking.

For a mechanical watch to keep the same time across all vertical positions the combined balance, staff, roller, collet and even balance spring must be as close to perfectly balanced as possible – to say nothing of the rest of the watch – which is challenging even with today’s modern hairsprings and specialised machines.

His invention rotated all the components most relevant to timekeeping along the same axis as the balance over a short period, meaning, theoretically, any arbitrary vertical position is the same as any other, when measured over a few minutes or more.

Interestingly, Breguet’s original patent for the tourbillon, and nearly all modern-day tourbillons, have a one minute period of rotation. However, most of the approximately 35 tourbillon pocket watch watches built during Breguet’s lifetime (and also tourbillon clocks and a chronometer) were of the four or six-minute variety, which reduces the load exerted on the mainspring.

Later, particularly in the late 19th and early 20th century, the tourbillon became associated with high performance timekeepers, in part because it was a natural fit for chronometry trials using the Plantamour rating system, which emphasised consistency across positions.

Today the tourbillon has been successfully industrialised in Switzerland and China, and more tourbillons are built in a single day, even by a single company, than during A.-L. Breguet’s entire life.

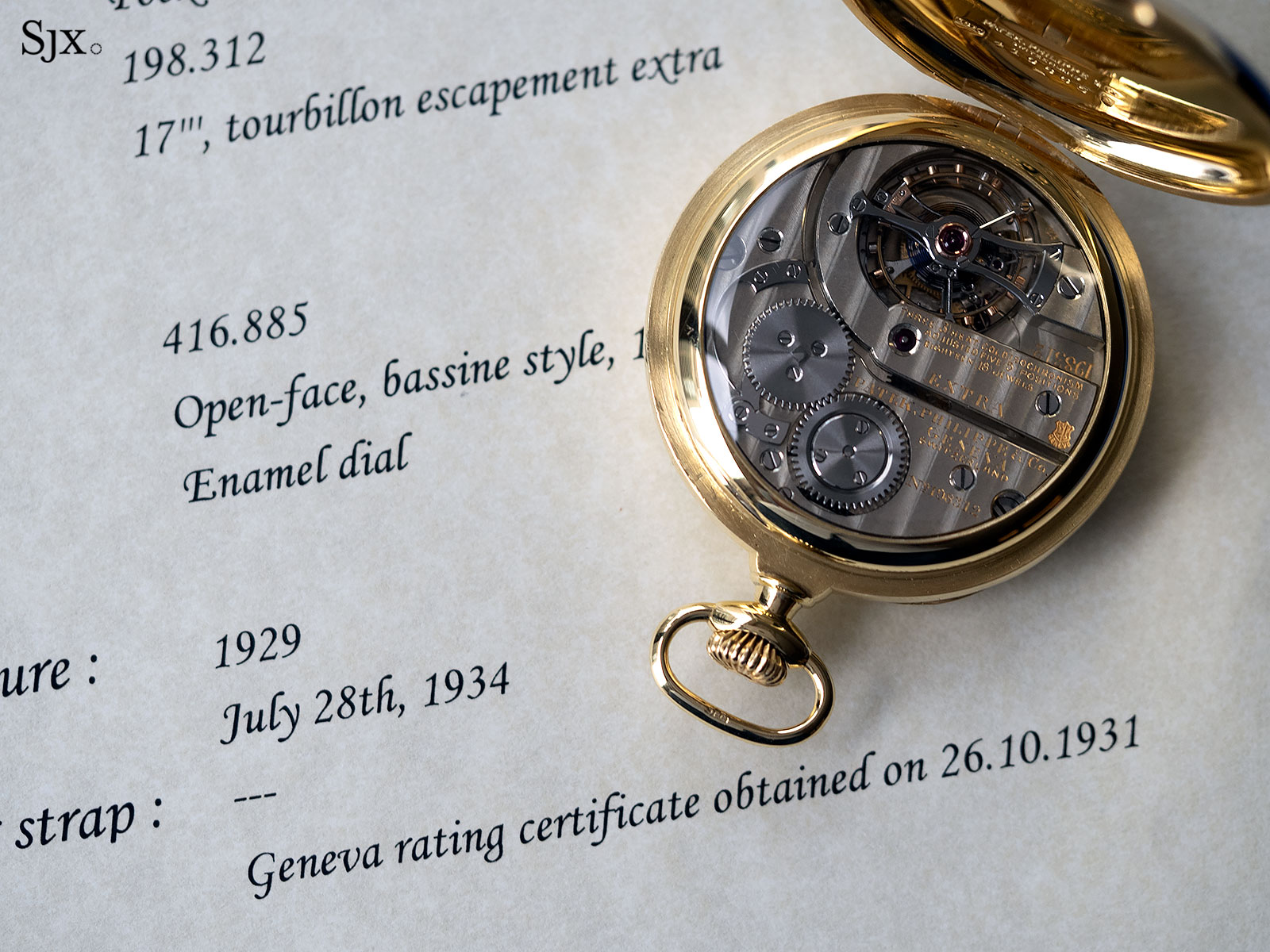
A Patek Philippe tourbillon tested by the Geneva Observatory.

The Watch

The watch going on the block at Sotheby’s is something of a celebrity, featuring prominently in the book Watches by Cecil Clutton and George Daniels. Clutton, the penultimate owner of this watch said “daily wear regularly shows a maximum variation in daily rate of five seconds, but generally very much closer, seldom exceeding two seconds.” While not remarkably impressive by today’s standards, the watch was already 150 years old at the time – over two centuries old now.

The  dial is immediately recognizable the as the inspiration for the modern company’s recent ref. 7225. The engine turned dial is solid gold with à grains d’orge – or barley corn – pattern and held in place by a single blued screw. All markings are engraved into the dial and filled with black wax, similar to the coveted champlevé enamel of some midcentury Swiss watches.

A cartouche at 12 o’clock proudly announces the presence of a Regulateur à Tourbillon or tourbillon regulator, only a few dozen of which existed at the time. Two seconds dials flank the main, and what appears to at first be a repeater piston in the crown stops one of the two seconds hands – stop seconds remains a rarity in today’s tourbillons. This “observation seconds” system involves a rudimentary vertical clutch.

Image – Sotheby’s

The exaggerated size difference between the Breguet style hour and minute hands follows the same philosophy as later regulator clocks, making confusion between the hours and minutes impossible. Both hands are set with aid of a key by a square in the centre.

Breguet’s books log the sale of this watch to Frédéric Frackman in May of 1809. Frackman was an agent of Breguet in Russia – an important market for the firm then and now – not the end customer.

The first owner was Count Alexey Razumovsky. In addition to Breguet’s usual double secret signatures either side of 12 o’clock, the dial is also signed “Comte Alexis de Razoumoffsky” between eight and four o’clock. This is the only known Breguet with a customised secret signature.

Just below, the power reserve indicator, which is always useful on a precision timekeeper, ideally it should me wound every 24-hours for best timekeeping. Though the watch should run about the same at any level of wind due to the chain and fusee.

Constant Force

The chain and fusee system resembles a bike chain in appearance and function, essentially changing gears as the watch winds down to maintain even torque. While already challenged in watches by better mainspring designs and materials during Breguet’s time, the chain and fusee survived all the way into the middle of last century in marine chronometers.

The movement uses pillar and plate construction, with its origin in clock movements, which was also retained in marine chronometers. Pins fasten the guilt three quarter plate to the pillars, instead of screws.

Each of the hundres of parts that comprise the chain were stamped out on a hand operated press. Obviously no one would do that today.

Unlike most verge fusee watches, which falter during winding, fusees of the era had the additional refinement of “maintaining power” by way of a small spring that takes over momentarily to drive the train during rewinding – it stores a few minutes of power in total. The silver tone wheel at the base of the fusee is the maintaining ratchet wheel.

The winding square.

Also like a marine chronometer, there are two squares on the back. The winding square sits on top of the fusee, while the setting-up square atop the barrel allows the watchmaker to tension the mainspring – never touch this.

The set-up square.

The dust cover only allows access to the correct square, and the watch should be wound with the dust cover closed to avoid mistakes. An arrow serves as a reminder that fusee watches (usually) wind counter clockwise.

Bifurcated Train

The fusee director the centre wheel, but after that the flow of power is hard to track as it occurs on the dial side, like a Chronometre Souverain. The left pinion carries the running seconds and drives the four minute tourbillon, which in turn drives the pinion carrying the stoppable seconds hand.

This early natural escapement doesn’t have two escape wheels, rather it has an escape wheel, with 12 teeth, and an escape pinion, with three. Each has three levels of teeth. The lowest teeth connect the escape wheel and pinion, the next impulse the balance directly, and the topmost interact with the sprung locking detent.

The latest natural escapement from the modern Breguet company, which I covered when discussing the upcoming sympathique does all of this on one level, thanks to modern design and manufacturing technologies.

The tourbillon cage must be poised as well, note the two sections of removed material to balance the assembly. Image – Sotheby’s

Breguet equipped his four-minute tourbillons with a free-sprung temperature compensation balance and an overcoil balance spring. The balance beats at 3 hz, which is remarkable considering even 2.5 hz was a high beat rate for the time.

The balance has three arms, which are brass on the outside and steel within. The mismatch in coefficient of thermal expansion between the who materials causes the arms to flex inwards as temperature increases (speeding the watch up) outward at low temperatures (slowing it down), which compensates for the effect of temperature on the balance spring.

Interestingly, the tourbillon assembly is modular, able to be pulled from the movement by removing two screws. Today, H. Moser & Cie uses this approach to streamline servicing. Oddly, the carriage appears unjeweled. In fact, they are but the usual arrangement is reversed, with the jewel bearings on the tourbillon cage and the pivots on the bridges.

The tourbillon module extracted from the movement. Image – Sotheby’s

Despite its obvious significance, this pocket watch arguably isn’t a “hot” watch in the current market. However, there are probably two or three collectors out there who will bring it well past the seven figure mark. Ownership of a watch like this comes with the responsibility of preserving an important milestone in humanity’s pursuit of mastery over time, a heavy burden.

Breguet no. 1890 has an estimate of CHF350,000-600,000 (US$430,000-960,000). For more, visit Sothebys.com.

Seiko’s evergreen mountaineering companion, the Prospex Alpinist, enters its fourth decade with its fourth major update. The 2025 edition gains an a longer power reserve, a scratch-resistant Diashield case coating, and — most notably — the return of vintage styling cues from the first generation, including the italic “Alpinist” signature on the dial.

The new generation (refs. SPB503, SPB505, SPB507) debuts in variants including the signature forest green, along with a limited edition of the outgoing generation exclusively for Singapore, Hong Kong, Macau, Malaysia, and Brunei in an icy white (ref. SPB532). Though it commands a slightly higher price than the outgoing model, the enhancements make it a more capable and durable field watch, keeping the value proposition firmly intact.

Initial thoughts

This year the iconic green-and-gilt Alpinist turns 30, though it seems to have aged gracefully, with the latest generation being the best since its original debut. Though the Prospex “X” emblem and “three days” script depart from the model’s earlier design, the return of the “Alpinist” script is a welcome touch.

Personally, I’ve always favoured its bigger brother, the Landmaster, which has higher specs for a higher price. But for most aspiring mountaineers, the much more accessible and conventionally attractive Alpinist is a better option.

Since early references of the Alpinist are incredibly difficult to find – at least by Seiko standards – the new Alpinist should prove to be the most appealing option for most collectors.

It’s not easy being green

While the Alpinist name dates back to 1959, the green and gold colourway and rotating compass bezel that we now associate with the collection were born in the ’90s. Shigeo Sakai – also responsible for the inflatable Seiko Airpro – designed three colourways for the 1995 Alpinist. The first two were black and beige, paired with a steel bracelet.

But there was a third model, inspired by Saki’s own almond green Mini Cooper (Japan was the Mini brand’s largest market at the time) paired with a brown strap that would ultimately define the collection in the minds of enthusiasts in the years to come.

The conventional wisdom within Seiko was that green dials would not sell well, yet the original cal. 4S-powered green Alpinist (SCVF009) held on until 2006 when the trio was replaced with the SARB Alpinists, which dropped the date magnifier. The ref. SPB121 debuted in 2020, reintroducing the date magnifier, but losing the colour-matched date window.

Thirty years of the Alpinist

Things have come full circle in 2025, with the return of the colour-matched date wheel with its gold outline, bringing the new Alpinist’s dial closer to the 1995 original than either of its predecessors.

Even the Alpinist branding has returned this year, though shifted upward in the form of a gold script rather than the original red printed text.

Seiko also changed the printing on the compass bezel from white to gold, a pleasing design choice that seems obvious in hindsight.

Historically, the green Alpinist was always accompanied by two other references, one in black and another in light cream or grey. This time, Seiko is trying something different with brownish-black and blue-green dials.

In theory, the black SPB505 should be the most commercially viable of the three, especially since it comes with a bracelet, though the blue-green SPB503 is arguably the most striking. Of course, the iconic green SPB507 is the one that most appeals to nostalgia.

The case is the same 39.5 mm in diameter as the original, and still measures a comfortable 46.4 mm from lug-to-lug, but it’s now half a millimetre slimmer. The hardy 200 m water resistance rating and reassuring screw down crown remain, accompanied by a display case back, now printed with the Alpinist logo.

The most significant upgrade, however, is probably the addition of Seiko’s ultra-hard Diashield coating, which now protects the case from scratches and scrapes, whether from rocky mountain passes or aluminium keyboards.

The no-nonsense cal. 6R55 is visible through a display case back, and boasts a full three days of power reserve, up about two hours from the last generation. That longevity is due, in part, to the use of MEMS manufacturing techniques to reduce the escapement’s weight – a feature once reserved for Hi-Beat Grand Seikos that has quietly trickled down to the cal. 6R family, differentiating these in-house calibres from Swiss peers.

The cal. 6R55 also has all the usual accoutrements that mark it as a step up from the brand’s entry level movements: stop seconds, hand winding, and a quick-set date.

A swan song

The new Alpinist collection launches alongside an 800-piece limited edition variant of the outgoing SPB121 with subtle gold accents around the bezel, exclusive to the Thong Sia Group, Seiko’s distributor in Singapore, Hong Kong, Macau, Malaysia and Brunei.

Key facts and price

Seiko Prospex Alpinist 6R55-00P0
Ref. SPB503 (Blue-green dial on bracelet)
Ref. SPB505 (Black-brown dial on bracelet)
Ref. SPB507 (green dial on leather strap)

Diameter: 39.5 mm
Height: 12.7 mm
Material: Steel
Crystal: Sapphire
Water resistance: 200 m

Movement: Cal. 6R55
Functions: Hours, minutes, seconds, date
Frequency: 21,600 beats per hour (3 Hz)
Winding: Automatic
Power reserve: 72 hours

Strap: Leather strap (SPB507) or steel bracelet (SPB503 and SPB505)

Limited edition: No
Availability: At Seiko boutiques and retailers, and Seiko’s online store.
Price: US$900 (SGD1,290.60) on leather strap, US$995 (SGD1,417) on steel bracelet excluding taxes

Seiko Prospex Alpinist Thong Sia Group Exclusive Limited Edition
Ref. SPB532

Diameter: 39.5 mm
Height: 13.2 mm
Material: Steel
Crystal: Sapphire
Water resistance: 200 m

Movement: Cal. 6R35
Functions: Hours, minutes, seconds, date
Frequency: 21,600 beats per hour (3 Hz)
Winding: Automatic
Power reserve: 70 hours

Strap: Textile strap with fold over clasp

Limited edition: 800 pieces
Availability: At Thong Sia Group boutiques in Singapore, Hong Kong, Macau, Malaysia, and Brunei
Price: SGD1,127 (about US$870) excluding taxes

For more, visit Seikoboutique.com.sg.

This was brought to you in partnership with Thong Sia Group.

In a past story, we explained how multiple mainspring barrels can be paired in parallel or in series, for either lengthening a movement’s power reserve or increasing the torque discharged into the going train. In this article we expand on this topic to analyse the inside of the barrel by exploring how mainspring size balancing influences the torque output and power reserve.  

Enthusiasts tend to throw around the loosely-defined term “mainspring packing” — especially when criticising a movement’s unsatisfying power reserve. This term refers to how a watchmaker can get a higher power reserve by balancing a spring’s dimensions and the space it occupies inside a barrel. While this sounds simple, the reality is more complicated. 

Skeletonised barrel showing the tight coiled mainspring inside the Piaget Altiplano Tourbillon Concept.

In order to set the record straight, it’s necessary to analyse the topic thoroughly. This requires getting a bit technical, but an interpretation is included for those less interested in the underlying maths. This theory-heavy deep-dive tries to unravel the concept of mainspring packing and explores why optimisation is not a very straightforward business.

The core elements

This section covers the basics of mainspring and barrel geometry and establishes their relation with power reserve and torque. In order to see how specific dimensions affect both torque and power reserve, we will resort to some known functions and a little geometrical reasoning. Equally, we need to take into consideration that the available space inside a barrel is finite. Since it is spanned by the coiled strip, sizing the mainspring implies some trade-offs. In short, one can either have a thick mainspring with few coils, or a long spring but with thinner coils.

The analysis will mainly revolve around these four notations: L – the total length of the coiled spring; e – the thickness of the spring, N – the number of developing turns of a mainspring, from fully wound to fully depleted; K – the stiffness of the coiled spring of rectangular section.

The running power reserve is in fact analogous to the number of developing turns N. A large N value is synonymous with a long power reserve. In order to see how N really scales with the two variables e (spring thickness) and L (spring length), we start off with some geometric considerations.

Figure I. The mainspring in fully wound and unwound states.

Figure I shows the two extreme states (wound and unwound) of a mainspring barrel. Since the coils physically span the barrel space, we can find by geometric reasoning both the number of turns of full charge N’ and the number of turns of a depleted charge N”. R is the interior barrel radius, measured from center to wall.

The other radius r is not the arbour radius, but rather the realistic radius of the innermost mainspring coil. A spiral spring would fracture or permanently bend, should it be coiled fully around the barrel arbour. As such there is an interior limiting factor here, a circular area of radius r that will never be occupied by the spring. 

The complete mathematical reasoning is shown bellow in Figure II, where we link set radiuses R and r to the number of turns N — which then gives us the final expression of available turns function N in terms of just e, L, R and r. 

Figure II. Deducing the total number of developing turns.

For the barrel torque, we will refer to the known formula of elastic moment for a coiled spring of rectangular section, shown in Figure III. The formula K shows the stiffness of the system. This value multiplied by an arming angle gives the torque discharged into the going train. Young’s modulus E and the height of the spring h are treated as given constants in this analysis. We will refer to K as the stiffness function while conspicuously doing away with the complete torque expression involving the arming angle, since that is irrelevant to the spring geometry we’re considering.

Figure III.

Thus we have established two functions, each dependent on pairs of (L, e) and related to either the torque of the mainspring or its running time. Our goal here is to find some expressions for (L, e) which give us (separately) the largest stiffness K and the longest running time N and see if and how those values relate to each other. And there is no better tool for it than calculus. 

A failed initial method of approach

This section describes my first method of approaching mainspring size optimisation, which ultimately failed. When thinking of getting the best results for L and e pairs, I resorted to a straightforward method, making use of the equations established earlier. Later I realised the approach was flawed, but the fact that it failed is significant; it tells us that balancing mainspring sizes is a more layered matter that it initially appears. The failed experiment is covered in the following.

In multivariable calculus (where two independent variables influence the same equation) there exist constrained optimisation problems which are most easily solved using the method of Lagrange multipliers. 

An example of such an optimisation problem is the following: what is the maximum possible area of a rectangle of unknown side lengths, knowing that it has a set perimeter. This means that the sum of its sides is some fixed constant (the constraining function) and we need to find the optimal values so that our rectangle’s area reaches a maximal value. 

This sort of problem is usually solved by using Lagrange multipliers, as we try to find some linear dependence between the gradient vectors of the given and constraint functions. Leaving the mathematical jargon aside, this is usually a very useful way of finding maximal (or minimal) solutions to a multivariate expression. 

This method initially appeared to cater well to the mainspring problem. We look  to find both the optimal L and e for either a long power reserve N or a stiff K— all while under the mutual geometrical constraint of the finite barrel space. In other words, we want to find optimal pairs of mainspring width e and length L by separately maximising the N and K functions with regard to the finite available barrel space. 

Figure IV. The multiplier method setup.

For those interested, the equations above in Figure IV show how the system was initially set up. First we have the two gradient vectors, with the partial derivatives of N and area function, the product of e and L. Then a suitable scaling parameter λ is found — provided that the two vectors are indeed linearly dependent. The equations are then solved, hopefully yielding the pair (L, e) which serves as an extremum point for our N function. The process is a little abstract and unrelated to horology, but useful nonetheless.

The Lagrange multipliers method yielded plainly unusable results. The constraining function relies on a simple geometrical fact: the area spanned by a coiled mainspring of rectangular section is Le (length times thickness), which remains constant. But what is, in fact, that constant?

Looking back to Figure I, it looks like it might just be the difference between the area defined by R and the small circle area defined by r. This couldn’t be more incorrect, since there needs to be some space left for the spring to move around, from wound-to-unwound and vice versa. This free space being an unknown value in itself is one of the reasons the Lagrange multipliers reasoning fails. 

Applying the method only yielded the degenerate result of N=0 (or e going to infinity). This was traced back to an engineer’s worst nightmare — mathematical rigour. After a more thorough analysis of N as a function, it appears that it is inherently unfit for the Lagrange method, due to issues having to do with bounds and regularity. 

The nightmare worsened when I noticed the same fault with the K function as well. In other words, there is no way to get optimal pairs of both L and e for either function. 

This approach’s failure does tell us something though: the relation between L, e, K and especially N is not a straightforward one, and there is no instant wonder result for building a theoretically optimal mainspring. Thus we proceed to investigate each function, piece by piece. 

Back to more classical approaches

This section takes a different approach at studying how mainspring length and thickness influence both the stiffness and power reserve, by reviewing some of the initial assumptions. Looking back, there was one other error which plagued the reasoning: I initially considered the spring width e a true variable, to be found in the same manner as L. In doing that I overlooked the fact that e is realistically constrained by stress/strain relations. 

A thick beam can’t bend very much without permanent plastic deformation and even fracture, and we need many circular coils for a spring. Surely there must be some hard constraint on the strip thickness, hopefully also related to the barrel system geometry. There is one parameter, r, which is a strong contender, since r is practically linked to the elastic limit of the innermost coils. 

Leopold Defossez suggests that a ratio r/e of 16 works very well as a constraint, since the spring deformation during coiling-uncoiling around the arbour remains elastic. A ratio of 16 just means that the interior radius is sixteen times larger than the spring thickness. The ratio implies a direct relation between e and the inner barrel arbour radius r — meaning e is no longer a variable, but linked to parameter r.

In seeing that e is no longer a random variable, I resorted to just deriving N in terms of L (which here is possible, all rigour considered). Setting the derivative of any function to zero gives an extreme point of the function, which can be either its minimum (for convex functions) or maximum (for concave functions). Checking that N is indeed concave, when setting its derivative to zero (first row) we should find both the peak of N and its root L. This actually yielded a good result — the expression of L in terms of R, r and e (second row) which gives a maximum value N (fourth row). The computations are shown below, in Figure V.

Figure V.

Also, when multiplying this newly-found L by e (third row) we get the barrel area the spring occupies — which is exactly half of the total area available. Plugging this back into N gives us the maximum power reserve given by a mainspring of thickness e, lodged inside a barrel of R and r. The expression is consistent with that found in textbooks, although newer ones don’t go to the length of explaining its provenance. 

And now let’s consider the r/e ratio more thoroughly. We’ll call it α and rewrite all our important expressions in terms of it. We write N, L (specifically the expressions we just derived) and K in terms of α and immediately see some interesting things. 

Figure VI. Introducing α and ratios.

As α goes up, so does N in a linear fashion (third row). At the same time, K goes down very fast, since the expression includes the fourth power of the inverse of α (fourth row). It seems, pleasingly, that some relation between N and K is only dependent on this value α, all other factors being kept constant. 

The beauty of this is how all our relations remain valid, regardless of α’s value. The area spanned by the mainspring remains the same, and N and K only change with regard to α. By plugging in different numbers, we get the the maximum power reserve and the associated stiffness for the same set of constant construction parameters — R and r. In other words, we are now really talking about “mainspring packing”.  

The last two rows of the  equations above show the ratios between two Ns of different α and two Ks of different α. When keeping the R and r constant, both equations reduce to ratios in terms of just α. This gives us an interesting system to play with. 

While in the past the lowest admissible value of α was 14, due to advancements in material science and manufacturing, the lower limit today is more in the vicinity of 10. By title of example we can consider α to be 12, 14 and 16 — and observe the variance in the running time and stiffness of differently sized mainsprings spanning the same barrel.

Discussion of results

This section concerns the final results of our analytical endeavour. We see how by incrementally varying the thickness of the mainspring, both the power reserve and stiffness are affected (but very differently). The reduced ratios below should help in explaining the interesting relationships between different “mainspring packings”.

Figure VII. Balancing power reserve and torque.

Figure VII shows K12 is 85% stiffer than K14, and a staggering 216% stiffer than K16. This means that a mainspring of thickness r/12 is more than three times stiffer than another of thickness r/16. Now let’s look at the different ratios of N. Here the ratios are not as sharp; N12 is 85% of N14 and only 75% of N16.

The ratios are indeed telling. Varying α from 12 to 14, decreases the power reserve by 15%, but increases the potential torque output by 85%. It looks like a fair trade, since subtracting 15% from a standard power reserve of say 72 hours leaves us with around 61 hours. This still is a comfortable running time and the barrel torque is almost doubled. 

Considering an even sharper variation, from 12 to 16 makes for a 25% reduction in power reserve, but offers over three times the torque. So if the slim mainspring would run for 72 hours, the thicker one would only run for about 54 hours, while exerting thee times the torque. In this case, the stiffer mainspring would be just one third thicker than the slim one — not a huge variance, but with great effect. 

In real life, when going about building a mainspring barrel, watchmakers and engineers probably start by fixing R, since it is constrained by other movement and gear train dimensions. Then the desired N number of developing turns is set. The inner radius r can be then found early on as well and usually is one fourth to one third of R. Based on that, α is then determined and some e is found to satisfy it. This makes sure N is indeed maximal for the imposed barrel radius R. The spring however doesn’t have the highest torque output possible.  

This initial result can be tweaked for movements which prioritise a higher torque output: chronographs, perpetual calendars, tourbillons etc. In that case α can be slightly decreased by raising e, leading to a healthy gain in mainspring stiffness, while sacrificing just some of the power reserve. 

As the ratios show, any increase in thickness can go a long way in increasing the spring stiffness, while the power reserve is not decreased too much. The relation between r and e gives quite a large degree of freedom (α is not set to natural numbers only), so there is a wide theoretical range of torques and power reserves that can be obtained from one barrel size. In the real world, watchmakers are only limited by the choices offered by spring manufacturers, who produce springs in normalised sizes.

Another important takeaway is that there is a maximum number of developing turns associated with any given barrel size. So for any barrel to have the longest possible power reserve there can be found some exact values. This is not the case with stiffness. Function K has no maximum in terms of neither L nor e. So trying to get a stiffer spring for stronger torque always means straying away from the “perfect” power reserve for the given barrel size.

Limitations of the analytical method

As is often the case with purely theoretical reasoning, the results and conclusions drawn may not line up exactly with empirical evidence. For example, due to experience, watchmakers tend to fill as much as 55% of the interior barrel space with the coiled mainspring, while theory suggests that 50% is optimal. The difference is minimal, but deviates from the theoretical result due to practical experience. Watchmakers usually chose a length that is 1.2 times larger than the analytically determined optimal L, which conceivably leads to the increase in occupied barrel space. 

There is also the issue of uneven development of the coils inside the barrel. Much like with hairsprings, the mainspring doesn’t uncoil truly concentrically, leading to a real-life number of developing turns that is smaller than the intended N. To account for this behaviour, a small corrective factor (about 0.002 to 0.004) is added to e during the computations.  

To end this lengthy analysis, I must say this only scratches the surface of the quest for mainspring barrel optimisation. Engineers and watchmakers have to take note and study many other aspects of the motor organ, from spring material fatigue and magnetism resistance to lubrication, along with barrel wall thickness and side pressures on the wall and inner arbour. An often overlooked component of the mechanical watch, the mainspring barrel is quite a fascinating system which is still being actively improved by movement constructors.