Mechanical escapements remain the most fascinating and enticing field of horological study even in the 21st century. At its core, an escapement has a simple purpose: restore lost energy to the oscillating organ while regulating the discharge speed of the going train – thus allowing for time measurement.

Straightforward as the concept is, executing an escapement well is a completely different affair. The escapement is perhaps the element of the mechanical movement that has undergone the most iterations since its invention. The reason is simple: escapements were, and remain, imperfect systems. In fact, the escapement is often the least efficient aspect of a mechanical movement in terms of energy transfer. That’s why watchmakers and engineers have devised innumerable variants in the search of the ideal escapement. 

Explaining escapement efficiency

In physics the efficiency of a system is the proportion of useful work done relative to the total work done by said system. The result, measured as a percentage, speaks to the energy conserved within the system. For example, an 80% efficiency means that 20% of the total available energy is lost, with the remaining 80% usefully conserved. 

That said, an efficient escapement isn’t necessarily chronometrically-potent, since there are more criteria, apart from energy conservation, which reflect in a movement’s accuracy. The way in which escapement parts impulse to the balance, the proximity of the equilibrium point and the degree of engagement – all play their respective parts in the chronometric traits of an escapement. 

Quantifying efficiency in escapements is not easy. Being a complex system, the escapement presents some challenges in its analysis. That’s why the system is often separated into its constituents and analysed from different points of view, which are then summed up for a total view of the system. 

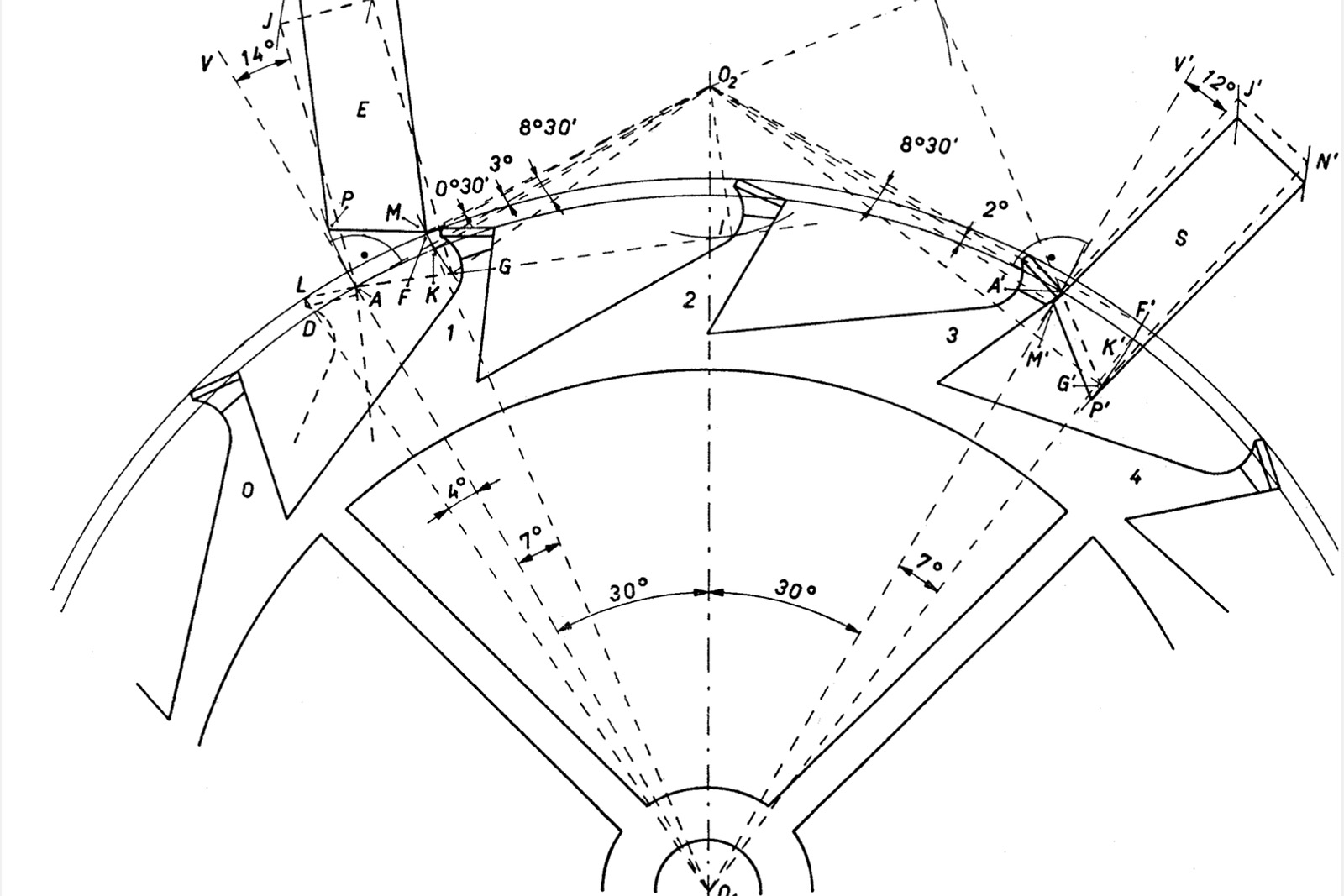
A plate showing the many angles that define an escapement’s geometry. Image – Théorie générale de l’horlogerie

A very sound definition of escapement efficiency was given by Dr. Olivier Laesser in his 2014 doctoral thesis Analyse, synthèse et création d’échappements horlogers par la théorie des engrenages (which translates as “Analysis, synthesis and design of watch escapements using gear theory”). His observation and conclusions were inspired by the work done in the 1970s by watchmaker-engineers such as F. Bonsack and R. Chaléat. In his thesis, Dr. Laesser broke down the total energy loss in escapements in three categories: losses caused by friction, dynamic losses and geometric losses. 

The friction losses are pretty self explanatory — pivot friction and sliding actions — they dissipate energy. The dynamic losses relate to the energy lost in accelerating the various escapement components, namely the escape wheel and lever from a standstill. Establishing these losses implies knowing the exact inertia moments of said components and it then requires some complex calculations of kinetic energies and semi-elastic collisions.

The geometric efficiency of an escapement is a more accessible concept. It only takes a static analysis of the system’s geometry and doesn’t require much calculation. The geometric efficiency reflects how much of the escape wheel’s travel is actually useful in parting impulse to the oscillator. The geometric efficiency shows how much energy is wasted from the start, by design, outside of frictional or dynamic losses.

Drops

Due to safety considerations, every escapement has “drops” (chute in French) intertwined with the lift phases. Escapements usually start out as locked, get unlocked by the balance, provide impulse to said balance and then get locked again. During the succession of events, the escape wheel usually advances by one angular step — the angle between two teeth. 

Drops appear as secure runs between the impulse and locking phases. In some direct-impulse escapements the escape wheel has to travel some degrees in order to catch up with the impulse pallet. Then it has to travel some more degrees after it disengages with the impulse pallet before it reaches the next locking. In lever escapements the escape wheel travels freely a certain number of degrees before locking. This dead-travel arcs are called drops and become the source of geometric energy losses in escapements.

Geometric efficiency 

After some preliminary physics considerations, calculating the geometric efficiency of any given escapement becomes pretty straightforward. Since escapements work in definite steps – one step is the advancement of a single tooth of the escape wheel – and the action is the same for every step, the geometric efficiency calculated for a single step applies to the escapement as a whole.

Total work done is by definition the torque M (measured at the escape wheel) multiplied by the total angle swept during one step. The useful work done is the sum of the work done for the entry and exit impulses of the escape wheel. By reducing M we find that the geometric efficiency actually depends only on the impulse angles and the angular step of the escape wheel (Figure 1).

Figure 1. The equation defining geometric efficiency

In the following we will go over some important escapements and try to determine their respective geometric efficiencies.

For conventional escapements, such as the detent or Swiss lever, impulse angles are easily found in classic horological literature and reproduced as such. For alternative escapements, the angles were determined through trigonometrical deductions based on patent figures and technical drawings. Thus the values are estimates and their accuracy is not absolute.

The 15-tooth Swiss lever escapement

Usually employed in conjunction with a 3 Hz (21,600 beats per hour) balance, the 15 teeth Swiss lever is one of the most basic escapements. Although defined by a complex geometry, the impulse angles are clearly established. Théorie générale de l’horlogerie by L. Defossez shows a model Swiss lever escapement with 15 teeth and notes equal 11° impulse angles, measured at the escape wheel. Similar values are suggested by George Daniels in his seminal work, Watchmaking.   

A plate showing the many angles that define an escapement’s geometry. Image – Théorie générale de l’horlogerie

During one full oscillation, the escape wheel advances one full step, or 24°. The escapement is unlocked at each vibration, then drops into the next locking after the impulse. The action is symmetrical and there is no drop right after the unlocking and before the impulse.

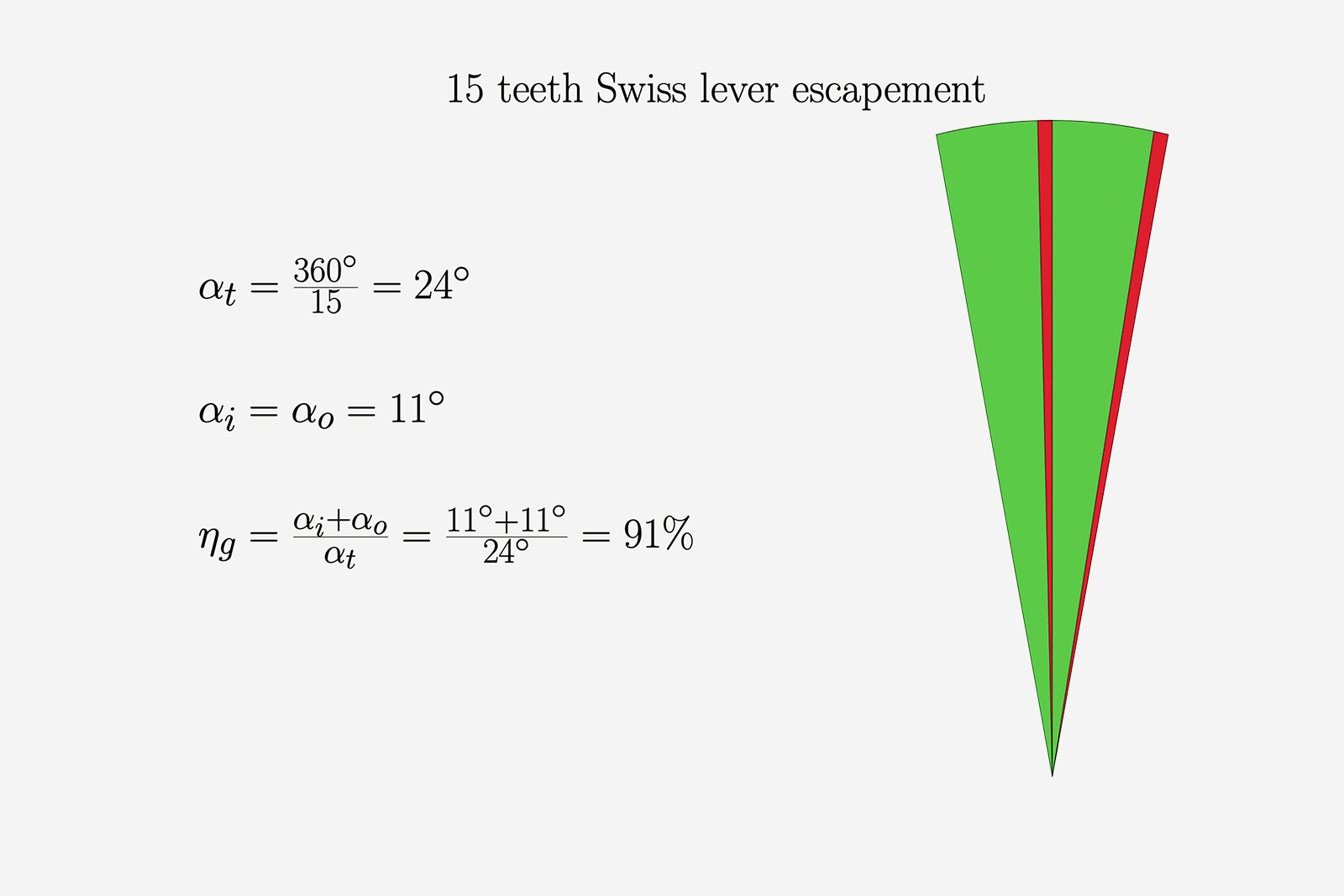
Figure 2

In applying the values to our formula we obtain a very high geometric efficiency of 91%. This means that the escapement geometry only accounts for a 9% loss of available energy, outside of frictional or dynamic losses.

Figure 2 shows a full angular step. The drop angles are shown in red, while the useful impulse angles are green coloured. Each impulse is followed by a drop.

The 20-tooth Swiss lever escapement

Escape wheels with 20 teeth are usually paired with 4 Hz (28,800 beats per hour) oscillators, making them more common in modern movements since 4 Hz is essentially the industry standard. An example of such an escapement can be found in the Mecanique Construction by Michel Vermot and Sebastien Dordor, which implies equal entry and exit impulse angles of 8°. The total angular step is 18°.

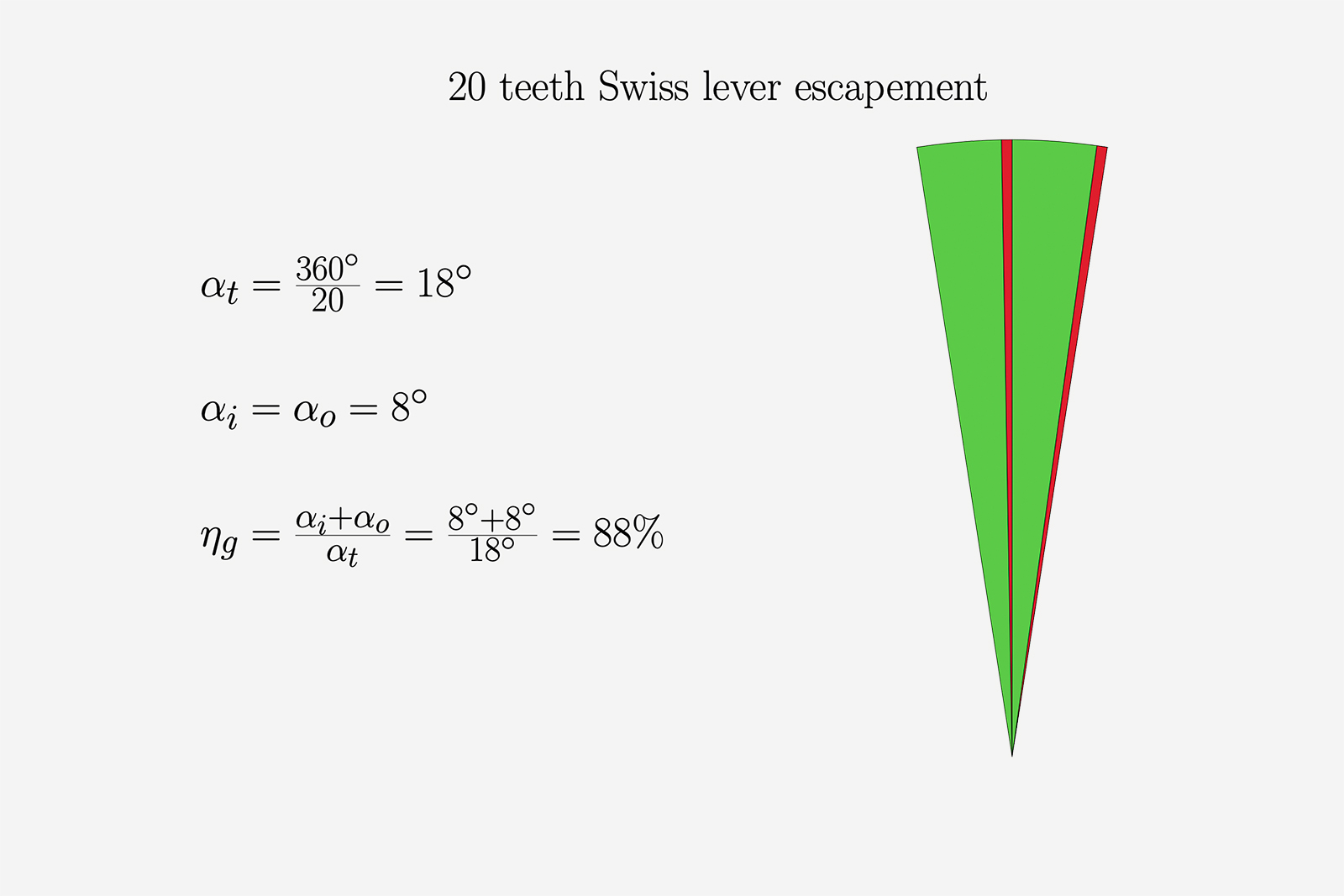
Figure 3

Figure 3 shows the geometric efficiency of such an escapement. By using our formula we find that the 20-tooth Swiss lever has a 88% geometric efficiency. This accounts for a 12% loss of available energy, slightly greater than the 9% loss in the 15 teeth Swiss lever. Since the drops are about the same, an observation can be made that for the same kind of escapement fewer teeth in the escape wheel are preferable for a higher geometrical efficiency. 

The 15-tooth detent escapement

Detent escapements with 15 teeth escape wheels are pretty common (as common as detent escapements go), with recently the Pagès Régulateur RP1 using such an example. Detent (or chronometer) escapements differ fundamentally from lever escapements since they part impulse directly to the balance wheel and there’s no anchor involved.

The pivoted detent escapement by Raul Pages. Image – Raul Pages

By design, detent escapements require a slight drop before impulse, as the escape wheel catches up with the impulse pallet, and then a second drop after the engagement breaks and the escape wheel locks. All things considered the drops are minute, together making up about only 1°. The chronometer escapement is a “dead-beat” escapement, since it only provides impulse once an oscillation.

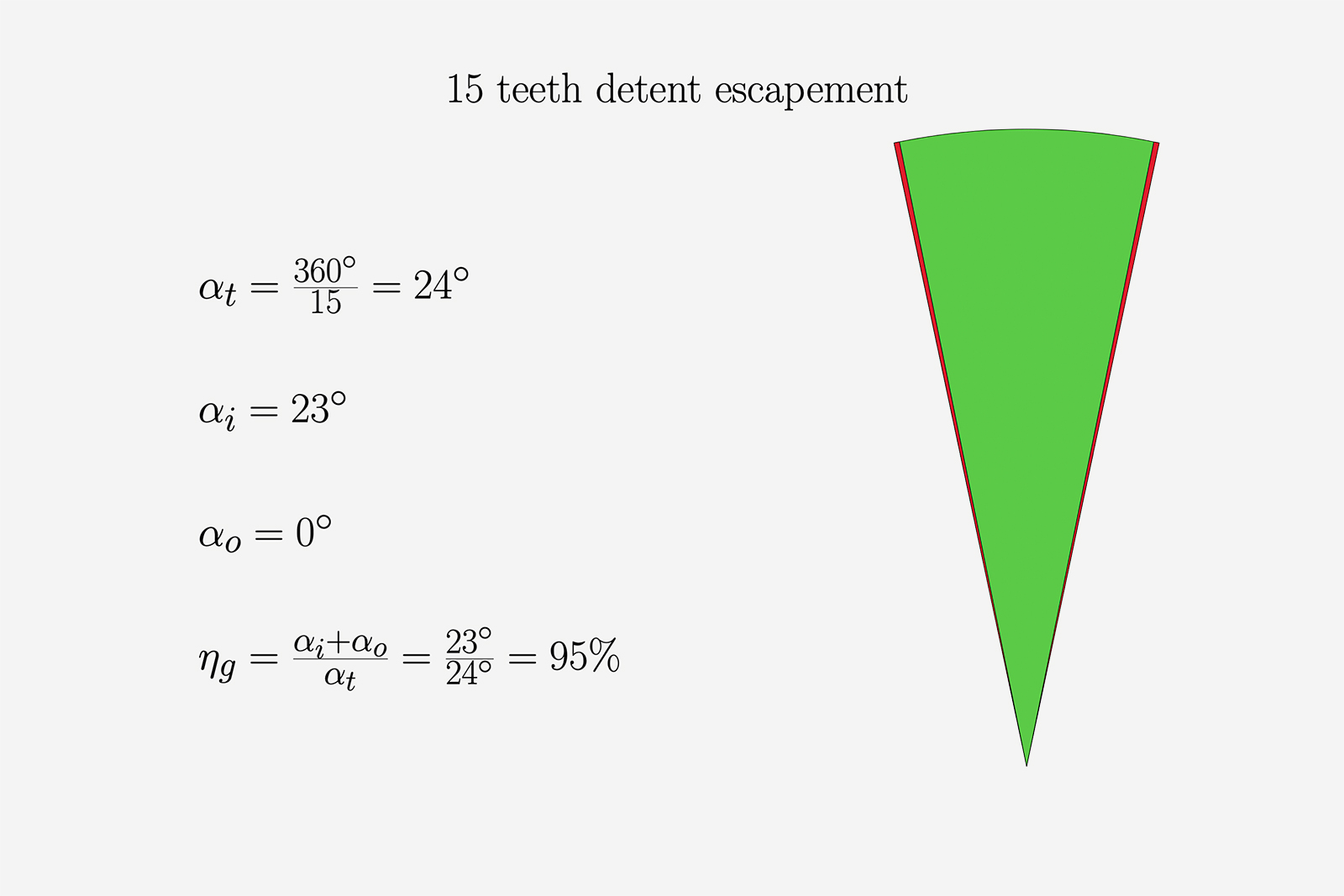
Figure 4

Figure 4 shows how geometrically efficient the detent escapement is, losing only 5% of the available energy.

As a slight digression, the chronometer escapement also has very small friction losses, as the components roll together smoothly, and equally small dynamic losses, since there is no intermediary lever to accelerate from standstill. This in turn accounts for the very high total efficiency of this sort of escapement, which is well known across the industry and among chronometry enthusiasts. 

The Grand Seiko Dual Impulse escapement

In early 2020 Grand Seiko launched an interesting alternative escapement, the Dual Impulse Escapement found inside the 9SA5 and now implemented across the wider 9S family. At its launch, the system was immediately compared to the Co-Axial escapement due to some apparent similarities. The Dual Impulse differs substantially from the Co-Axial, but is not truly novel. 

Conceptually, the Dual Impulse traces its roots to the Robin escapement. Invented by French watchmaker Robert Robin at the end of the 18th century, the namesake escapement works very much like a chronometer escapement, but it has a pivoted locking lever with two stones instead of a sprung locking mechanism. The design allows for a single impulse per oscillation, although the escape wheel gets unlocked at every vibration and travels very little during the “lost“ beat. 

In the early 2000s Renaud & Papi (R&P) devised a variant of the Robin escapement for Audemars Piguet dubbed the AP Escapement that was installed in the Jules Audemars ChronAP wristwatch. R&P’s version worked with a 6 Hz high-frequency balance and was endowed with a safety finger to prevent accidental unlocking. Other than the safety implements, the AP escapement operated almost identically to Robin’s initial design.

Abraham-Louis Breguet himself was preoccupied with improving escapements and one of his lesser known contributions to the field is the Breguet-Robin mixed-impulse escapement. Breguet took note of Robin’s design, but adapted the lever to accommodate a second impulse pallet which works just like in a conventional lever escapement. The result is an interesting mix of both the chronometer and the lever escapements. Breguet didn’t employ his invention widely and the Breguet-Robin escapement was largely forgotten.

The Grand Seiko Dual Impulse escapement in the 9SA5. Image – Grand Seiko

The Grand Seiko Dual Impulse is an almost exact adaptation of the obscure Breguet-Robin escapement, though the Japanese watchmaker did make some tweaks to the design and geometry. The escapement is hollowed out for lightness, optimising it for a high-beat oscillator of 5 Hz (36,000 beats per hour). The escape wheel only has eight teeth and the going train features five gears, instead of the customary four (including the escape wheel).

The direct impulse is considered here the entry impulse, while the indirect impulse is considered the exit impulse. The geometry is chosen so the escape wheel travels more for the direct impulse (about two thirds of the total step of 45°), than for the indirect impulse.

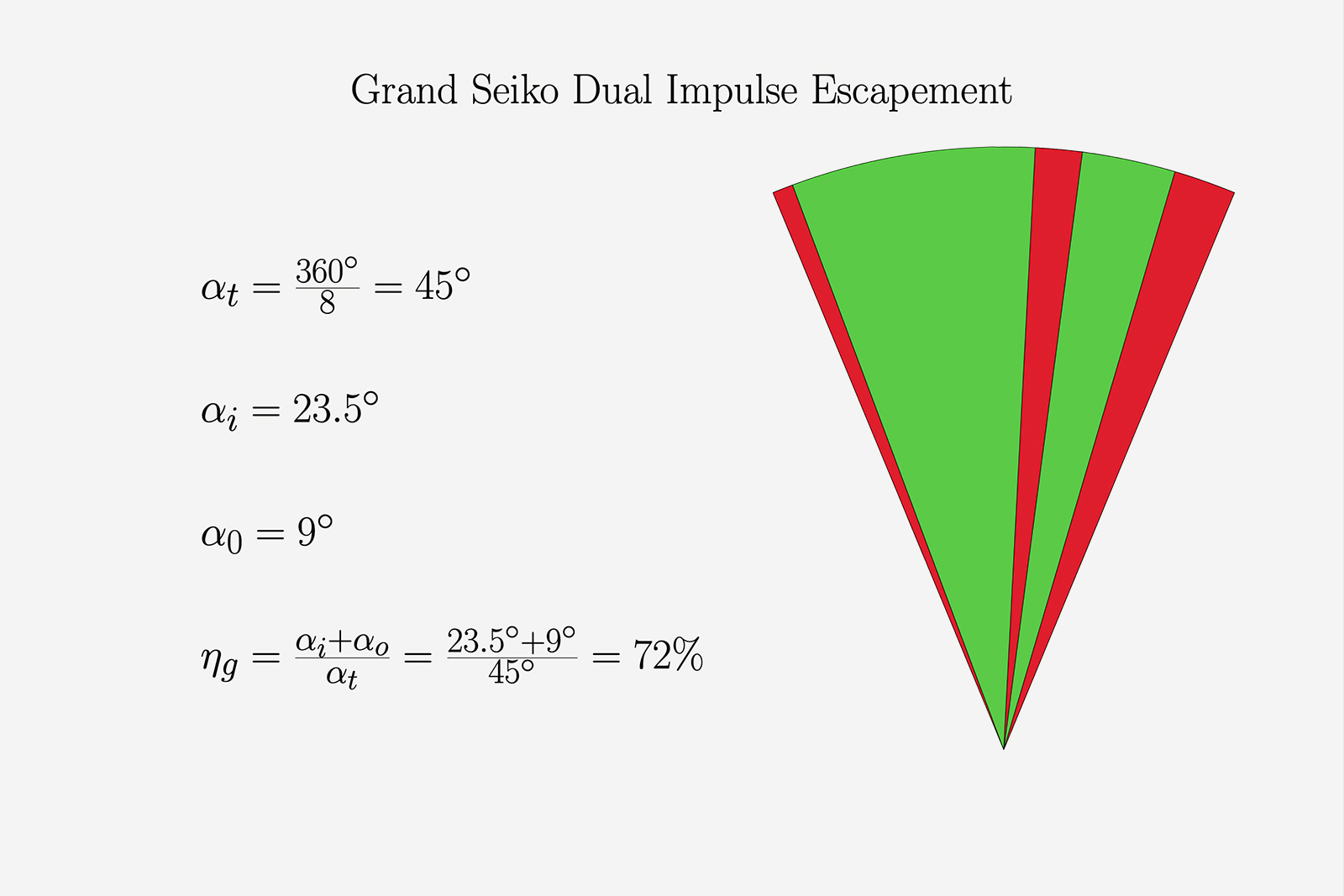
Figure 5

The impulse diagram can be observed in Fig. 5. Because the entry impulse is given in a direct manner, like in chronometer escapements, it requires drops before and after the actual impulse. The drops are more substantial here than in conventional detent escapements, due to the presence of the multi-purpose lever. 

The indirect impulse only takes about 9° of useful escape wheel travel, since the sharp escape teeth are not optimised and clubbed like in Swiss escapements. In this regard, the Dual Impulse is very much like old English lever escapements, which also feature pointy teeth and high drops. 

The 9S85 movement

The geometric efficiency of the Dual Impulse Escapement comes in at a slightly disappointing 72%, lower than Swiss lever escapements. While the frictional losses should theoretically be much lower than the Swiss lever’s, the dynamic losses would be comparable, if not greater.

As mentioned, the 9SA5 movements equipped with this escapement feature an additional mobile for accelerating the escapement, which suggest a rather low global efficiency. 

The Daniels Co-Axial escapement

One of the most famous modern escapement, the Daniels Co-Axial was always considered a capable and efficient escapement. Combining the reliability of the Swiss lever and the tangential impulse in the fashion of the chronometer and the Fasoldt escapements, the Co-Axial is a promising proposition.

Its origin story is well known: George Daniels developed the design during the ’80s and then sold it to Omega, which adapted it for mass production in 1999. Since then millions of movements have been equipped with the escapement, making it the most successful escapement in history after the Swiss lever. Daniels, however, likely took inspiration from a long-ago design for the Co-Axial.

Drawing of the “slim ” Co-Axial escapement. Image – George Daniels

The Co-Axial went through several iterations since it was first commercialised by Omega in 1999. The original geometry was altered in order to make the system more reliable. The geometric efficiency calculated for the Co-Axial here is based on Daniels’ own suggestions and notations from Watchmaking. The two superimposed escape wheels have the same number of teeth — 12 in the example given by Daniels, making for a 30° angular step.

The direct impulse is almost identical to the chronometer escapement impulse and takes 13° of the total escape wheel travel. The indirect impulse is similar and measures 13° as well (in Daniels’ example).

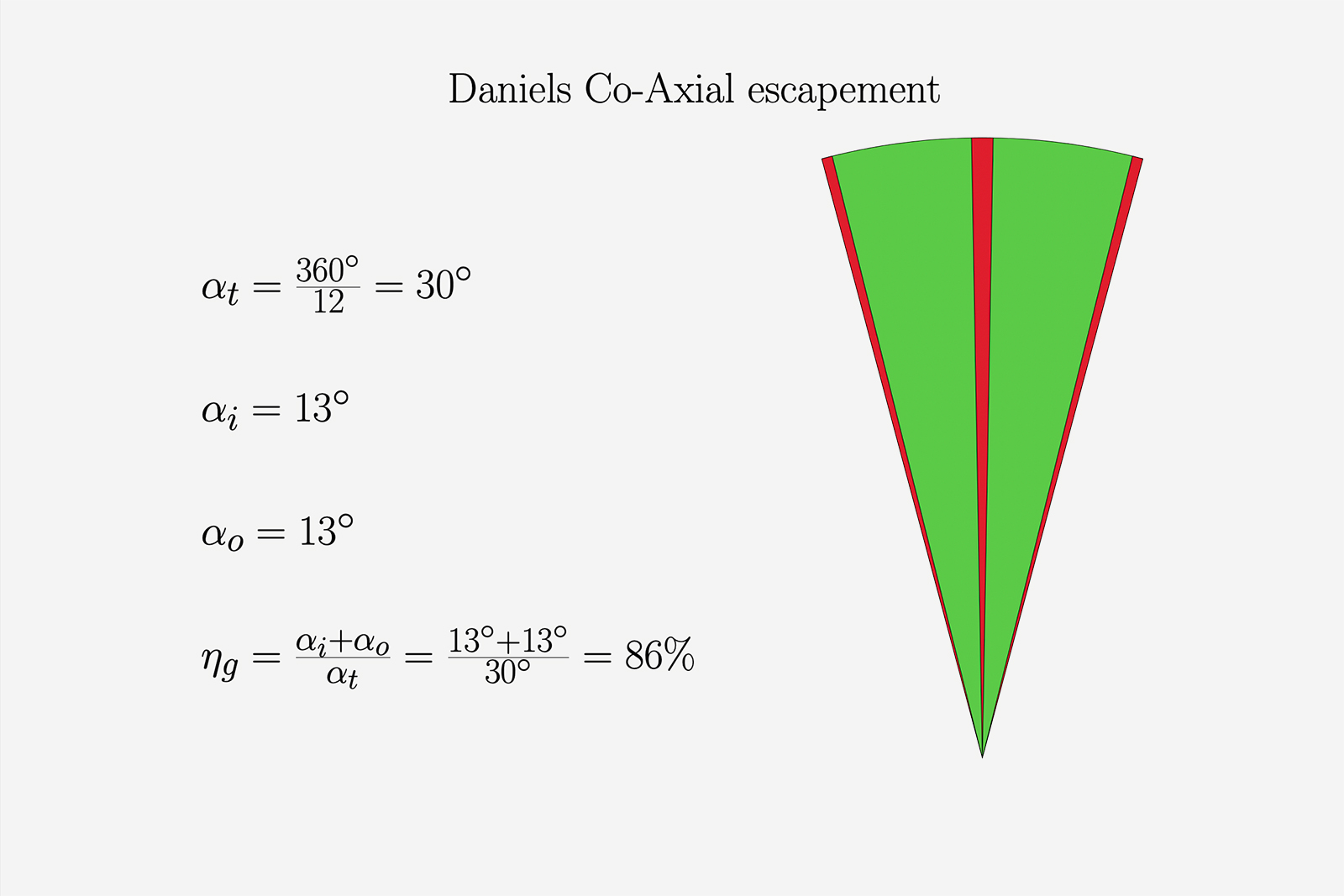
Figure 6

Figure 6 shows the impulse diagram of the Co-Axial escapement. The drops in red are symmetrical. Both the direct and indirect impulses are preceded and succeeded by equal drops, since in both cases the escape wheel has to catch up with either the balance or the lever.

The geometric efficiency of the Co-Axial comes at 86%. This makes it fractionally worse than the 20-tooth Swiss lever but reasonably better than the Grand Seiko Dual Impulse. 

Ulysse Nardin Dual Direct Escapement

The Dual Direct Escapement has only seen limited use since the first Freak in 2001, which was a watch notable for both its escapement and unorthodox movement construction. That said, the Dual Direct remains important in recent horology since it was the first ever movement component to be manufactured from silicon.

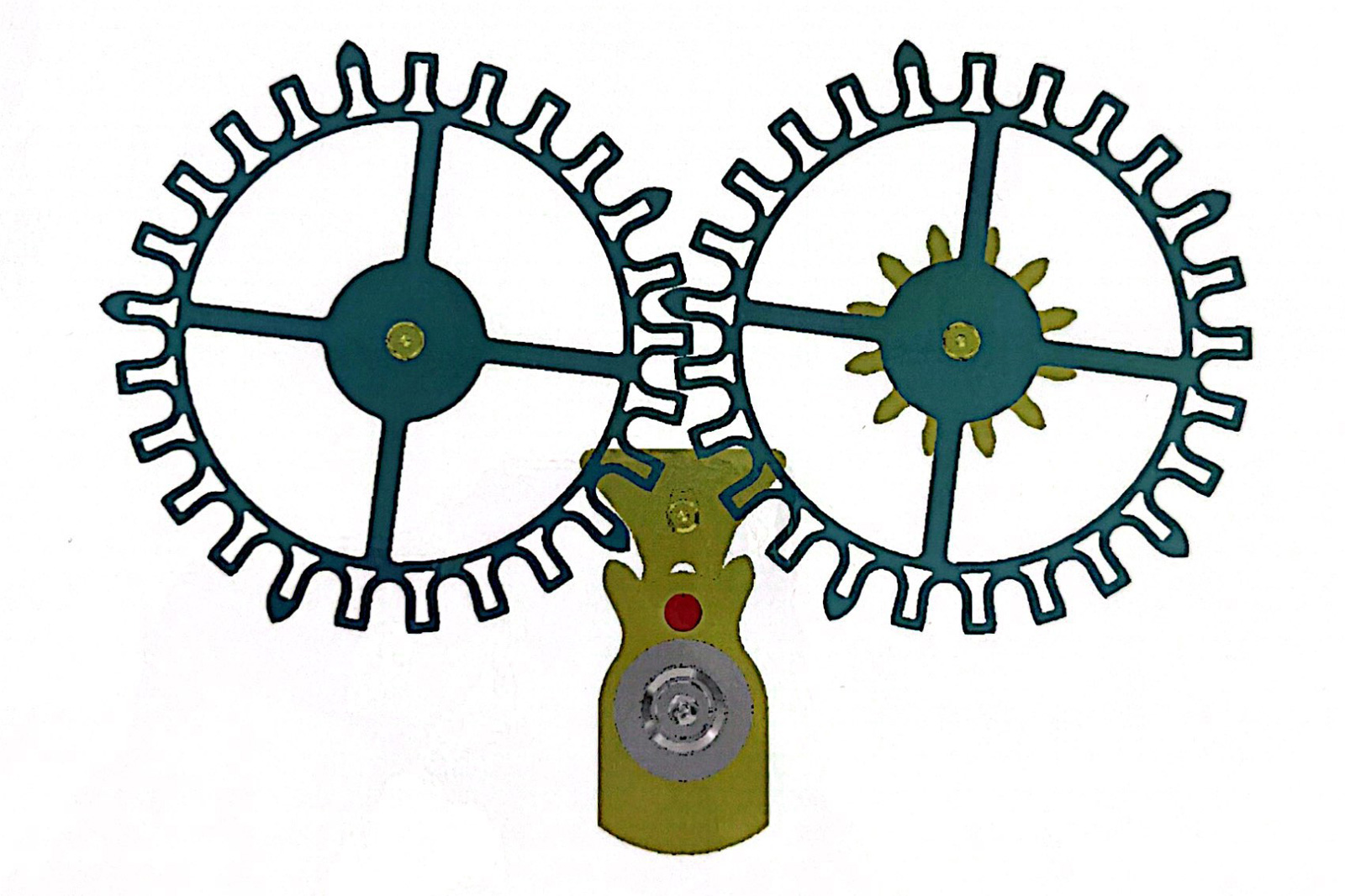
The Dual Direct escapement. Image – Ulysse Nardin

The Dual Direct bears great resemblance to Breguet’s natural escapement. Conceptually, the Dual Direct escapement is promising but in practice it was always impeded by reliability issues, which prompted Ulysse Nardin to fully replace the Dual Direct Escapement found in first-generation Freaks during service. 

The Dual Direct features two mirrored gears, each with only five active teeth. The non-standard arrangement doesn’t necessary complicate the geometric efficiency formula; because the two escape wheels are mirrored and perform exactly the same, we can attribute two impulse angles to the same escape wheel. During one oscillation each wheel advances by one tooth spacing and each parts impulse once. This is equivalent to one escape wheel parting impulse twice every oscillation for the same angular step. The spacing between the active teeth is a very large 72° step. 

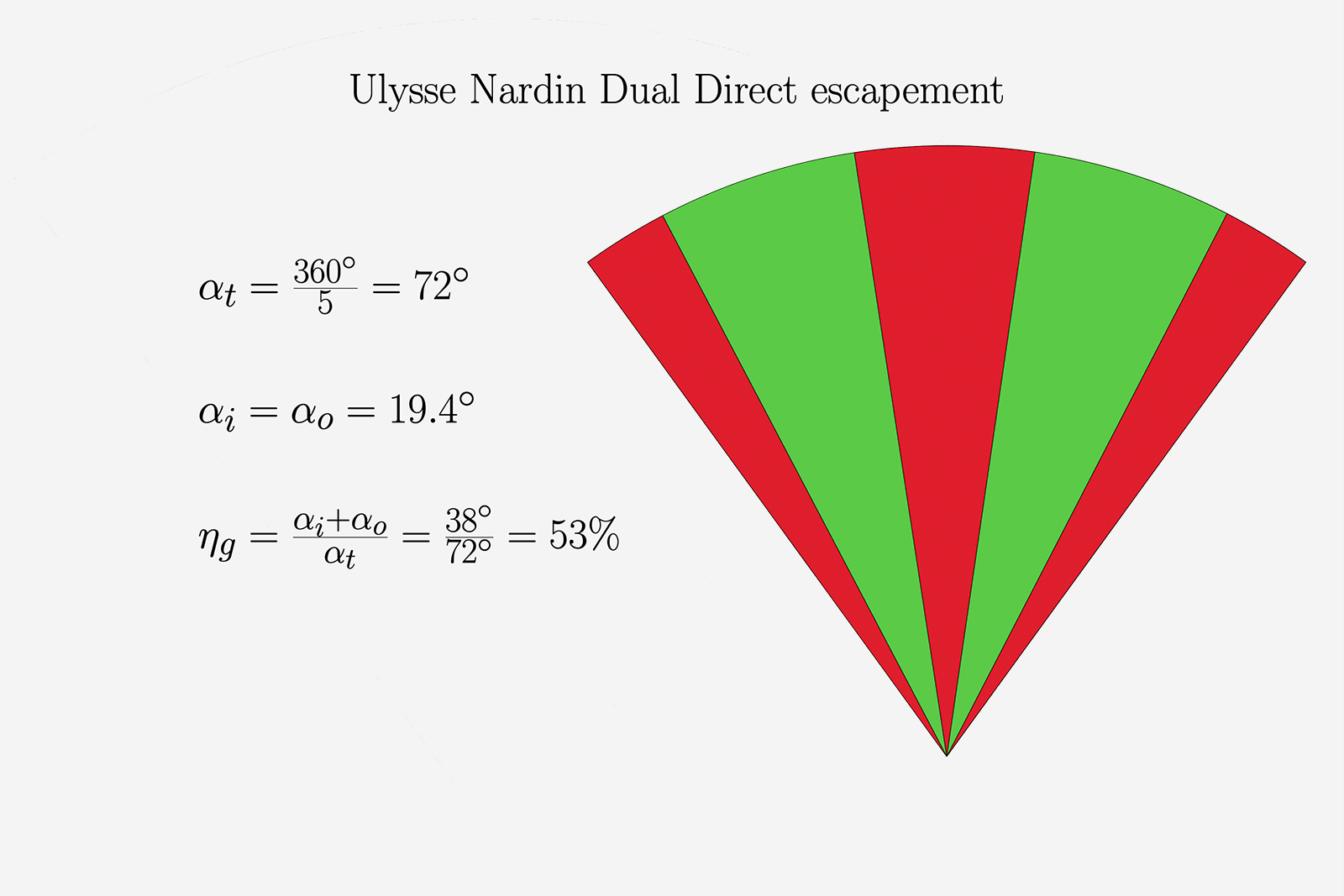
Figure 7

The Dual Direct escapement disappoints from a geometric efficiency standpoint. Figure 7 shows that the system has a very low geometric efficiency of just 53%. This means that about half of the system’s energy is wasted from the start, not counting frictional or dynamic losses. Since the escapement has two escape wheels geared to one another, the dynamic losses are amplified due to the added inertia. 

Compared to other direct impulse escapements like the detent or the Co-Axial, the Dual Direct has exaggerated drops (shown in red in Fig. 7) before and after the actual impulse. The widely spaced teeth and the proportion between the impulse pallets and the escape wheel mean that the two components intersect little in their trajectory, leaving much of the escape wheel travel unused. 

Comparing the escapements

Determining some important escapements’ geometric efficiencies is an interesting and insightful thought exercise. The analysis sheds some light into how some of these famous systems work, but also tell a tale of compromise in design choices.

The escapements on our list and their respective geometric efficiencies are put in better perspective in the chart from Figure 8.

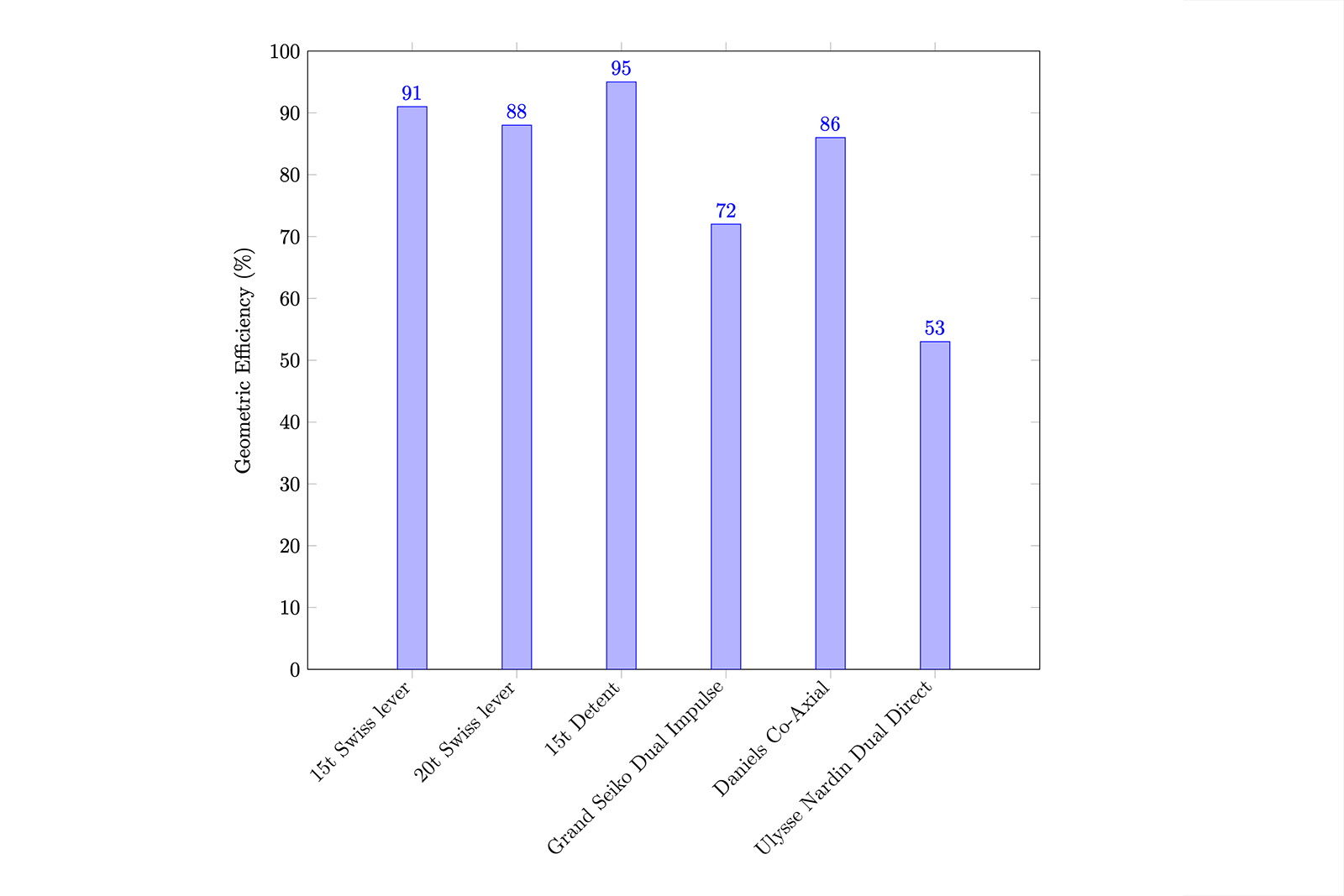
Figure 8

From a geometric standpoint, the best system is by far the detent or chronometer escapement. Although it is a dead-beat escapement, it makes great use of the available travel, losing only a small fraction of its energy. As mentioned, the frictional and dynamic losses themselves have small values, which fortify the detent’s position as an excellent escapement. 

The movement of the Raul Pages RP1. Image – Raúl Pagès

The two Swiss lever versions also feature surprisingly high geometric efficiencies, comparable even to the detent escapement. Promising as it is on paper, the Swiss lever is only geometrically efficient. Its frictional losses are especially great – hence the well-known need to lubricate the Swiss lever generously – and so are the dynamic losses that come from accelerating the large anchor from standstill, which consumes a fair share of energy.

The Co-Axial is comparable to the Grand Seiko Dual Impulse in the sense that both rely on complex geometries and multi-purpose levers, which can ultimately work against their geometric efficiencies. Classical escapements, like the detent or the Swiss lever, were refined over the years with both practice and theory, so their respective current forms are optimised as much as feasible. Newer, exotic escapement designs can be considered still “raw” in comparison, which might explain why their geometric efficiencies are notably lower.

Looking at the Co-Axial in particular, we might suppose the following: the lever action is similar to the Swiss lever’s. The two co-axial wheels make up for a greater total inertia, which points to very high dynamic losses – comparable or greater even than the Swiss lever’s. The Co-Axial’s friction losses remain small due to the direct nature of the impulses. But since the Swiss lever has higher geometric and supposedly dynamic efficiencies, we might speculate that the Co-Axial’s total efficiency is not much — if any — better than a modern Swiss lever. There are other considerations which make the Co-Axial a better escapement (like the low lift angle at the balance), but we’ll not go into detail. 

The least efficient escapement is the Ulysse Nardin Dual Direct. The absurd geometric losses speak of the innate design flaws and suggest that not everything can be reinvented with no regards to existing norms. Dr. Ludwig Oechslin, the Dual Direct’s creator, is undoubtedly a great scientist and watchmaker, with an iconoclastic approach that’s resulted in landmark timepieces. His approach wasn’t ideal in the Dual Direct, which nevertheless remains a brave attempt at reinventing the escapement. 

A first-generation Freak with its Dual Direct Escapement replaced with the Dual Ulysse Escapement

Parting thoughts

As mentioned in the beginning, the escapement is a complex system and can’t be properly analysed from a singular point of view. If the escapement were a patient, the geometric efficiency analysis would be akin to an X-ray: it outlines some important aspects, but it doesn’t give the bigger picture and doesn’t enter specifics. That is why a total escapement efficiency value is harder to obtain and most of the time is an estimate obtained through trials and experimentations. 

Also, an accurate timepiece doesn’t rely solely on an efficient escapement. Other important aspects are the oscillating organ itself, the hairspring and the consistency of torque from the mainspring to the escapement — all which have nothing to do with how well the escapement conserves the available energy. 

Energy conservation becomes important for power reserve management. An escapement that wastes the available energy recklessly will deplete the mainspring much faster than an escapement with better energy management. An efficient escapement can be advantageously paired with a weaker mainspring, which in turn doesn’t put that much strain on the movement as a whole.