The invention of the hairspring was among the greatest breakthroughs in horology, since its inception suddenly made mechanical timepieces portable, transforming clocks into watches. This not only marked the start of precision timekeeping, but also set mankind upon the long road to perfecting the accuracy of mechanical watches, arguably the most sophisticated pieces of kit on Earth at the time, when such precision was paramount for fields as varied as navigation, warfare, and astronomy.

The hairspring turned 350 years old in 2025 and we’re marking the occasion with a series of stories on the topic, including the story of the spiral hairspring and also the importance and evolution of the overcoil. Now we turn to temperature compensation and metallurgy in a two-part story covering the evolution of the hairspring materials up until metal alloys. More exotic materials and inventions will follow in Part II.

Elasticity and thermal expandability 

One of the fundamental factors in hairspring function is ambient temperature, simply because metal alloys expand or contract uni-directionally with a change in temperature. As a result, watchmakers used calorimetry, the science of temperature effects, and material science, specifically metal alloys, to their gain in advancing hairspring technology.

The equation below shows the relation between the initial length of a metal strip L₀, measured at a given temperature and the final length L_T after a certain change in temperature. 

The equation is often reduced to the first linear term (containing the α coefficient), since it suffices for small changes in temperature and instances where extreme accuracy is not needed.

This is not the case for sensitive instruments like hairsprings, so the quadratic correction term (with β coefficient and squared temperature change) is required. The full equation with the quadratic correction term has long troubled watchmakers when compensating for temperature.

While this equation does not hold exactly true for the Young’s modulus’ change with temperature, it offers a good understanding of the non-linear changes in the temperature-related behaviour of metals (an important observation, as we’ll see later).

Temperature’s effect on metal elasticity is generally the same: temperature increases result in the agitation of atoms within the metal, leading to bonds between molecules slackening to a degree — making for a change in volume on a macro-scale. The weakened bonds also mean the molecules don’t attract each other with the initial strength and the material as a whole becomes suddenly less rigid.

For springs, this means the stiffness constant, a function of Young’s modulus, declines. This directly influences the frequency of the spring oscillator. We discussed the exact relation between spring stiffness, balance inertia and oscillating frequency in a past story concerning mechanical watch regulation. 

The takeaway here is that a rise in temperature not only causes metals to expand, but also makes them less rigid. This is intuitive, since a continuously heated metal sample will become softer and softer, until a phase change will occur and the material will become molten.

The earliest hairsprings

When Dutch astronomer and inventor Christiaan Huygens (1629-1695) first presented his sprung oscillator, he described the balance spring as “an iron spiral”. While “iron” was probably an iron-copper or soft steel alloy, the material was rudimentary and initially chosen for its malleability and elastic behaviour, which fitted Huygens’ needs at the time. The first embodiments of the system featured simple wire coils and had one and a half to two turns.

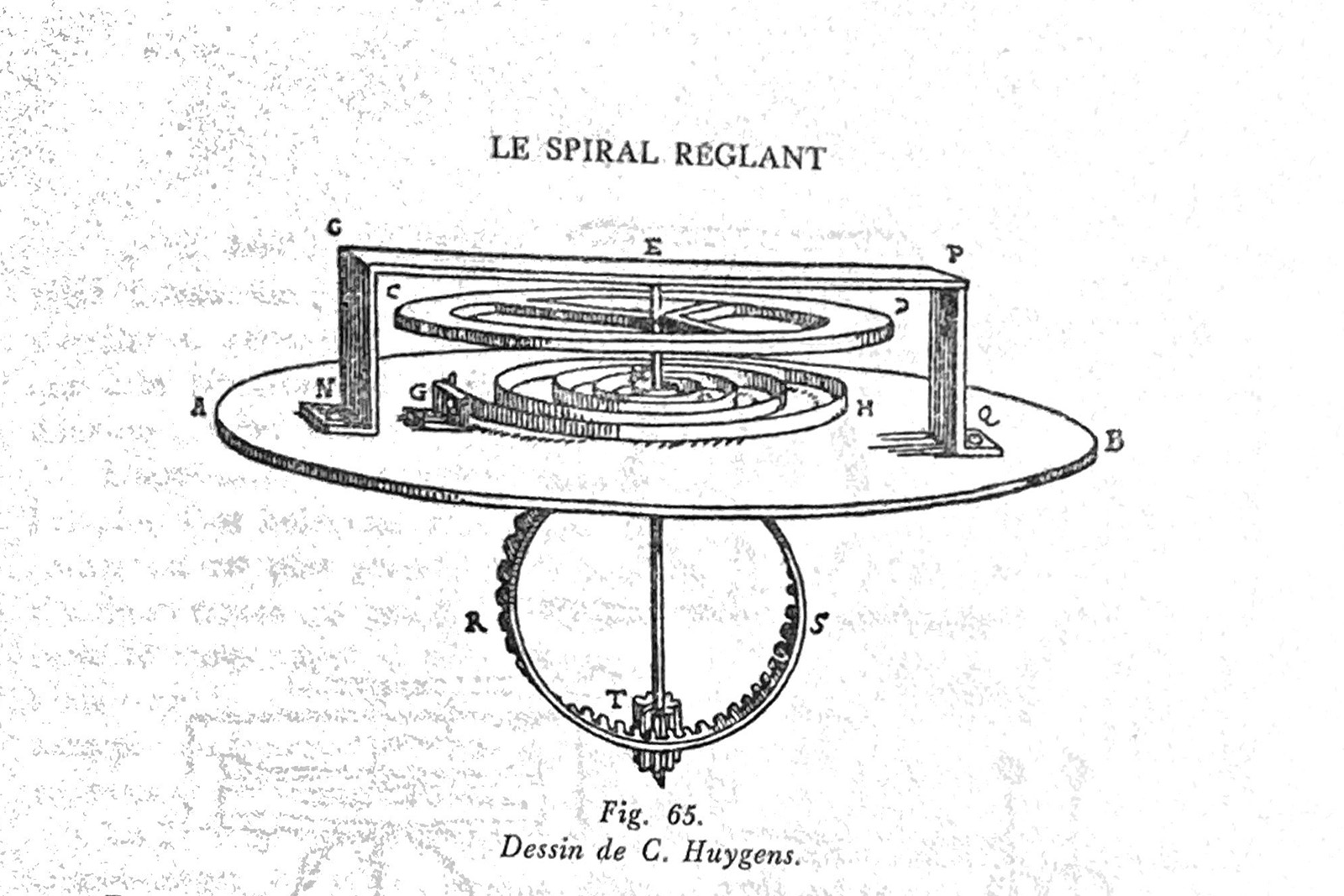As the spiral hairspring slowly became widespread, watch and clockmakers noticed the material of the spring was perhaps as important as its shape. They discovered that steel alloys (steel is a mixture of iron and chromium) were rather susceptible to both temperature changes and also to atmospheric humidity, which tends to unevenly oxidise the iron component. 

Over time watchmakers experimented with different types of steel alloys, mostly carbon steel. While more stable compared to the first rudimentary springs, the steel was still very sensible to temperature changes. Moreover, watchmakers discovered a new phenomenon, the gradual weakening of ordinary steel springs due to the molecules shifting and the general fatigue of the material. 

For untempered steels, molecules dislodged during the plastic deformations involved in the manufacturing process (mainly cutting, rolling, and flattening in the case of balance springs) tend to diffuse into the material over time. This can unevenly stiffen the spring. We have covered the topic in more detail with Rolex blue Parachrom hairsprings.

Another longterm effect, larger in magnitude than molecular shift, is the fatigue. Fatigue is a metric tied to the repeated stress cycles a given part is subjected to over a specific time period. As a component of any sort is subjected to cyclic loading and unloading, it develops small cracks and plastic deformations over time, which change its structure and stiffness. 

In the case of a high-frequency vibrating spring which charges and discharges a number times a second, the fatigue is exacerbated and it doesn’t take long for the hairspring to lose its initial stiffness and become weaker. As with the weakness induced by the temperature changes, the frequency of the oscillator falls behind, effectively making the timepiece run slower. 

The eminent English clockmaker and a champion of precision timekeeping, John Harrison (1693-1776) was among the first to heat temper and harden the steel hairsprings, according to R. T. Gould’s The Marine Chronometer: Its History and Development. The heat-hardening slowed the springs’ fatigue-related decay to an extent. The blue hue of old hairsprings is due to this heat tempering process, which covers the steel coils with a fine oxide layer. This byproduct of tempering also happens to protect the hairsprings against corrosion. 

Temperature remained still the most immediate threat to the day-to-day accuracy of sprung timepieces. Fellow English clockmaker John Arnold (1736-1799) experimented with steel but also with precious metal hairsprings. He favoured gold springs, which were not very sensible to temperature changes. But being a soft metal, gold was more susceptible to fatigue related loss of stiffness and could not be tempered. Similar trials involved palladium-alloy springs.

Abraham-Louis Breguet (1747-1823), among others, experimented with cylindrical glass balance springs, which he believed to be better than their metallic counterparts. His trial results were mixed, although the glass springs fared better in terms of temperature stability. But the brittle nature of the material, along with its increased shift effect made them unsuitable replacements for metallic springs. Moreover, the glass tends to form uneven micro-crystals inside its lattice, thus making the spring less homogenous and stiffer. This behaviour is known as devitrification. 

Temperature compensation and the secondary error

Since it became clear to watchmakers that coming up with a hairspring that was not susceptible to temperature changes was improbable, they moved their focus to trying to counter the effects of the unstable hairspring.

Watchmakers started off with the simple observation that balance springs weakened at high temperatures and stiffened at lower temperatures. Holding this as a given fact, they begun researching into compensation methods that would cancel out the troubling effect. 

As we’ve explained in a past story about mechanical watch regulation, the natural frequency of a spring-balance system is dependent on the hairspring’s stiffness and the balance wheel’s moment of inertia. The shorted version is that for the same given spring, a balance with a higher moment of inertia beats slow, while another with a smaller moment beats conversely faster. 

Using this piece of information, watchmakers reasoned that a dynamic balance, whose moment of inertial would change in relation to temperature, could counteract the change in spring stiffness. 

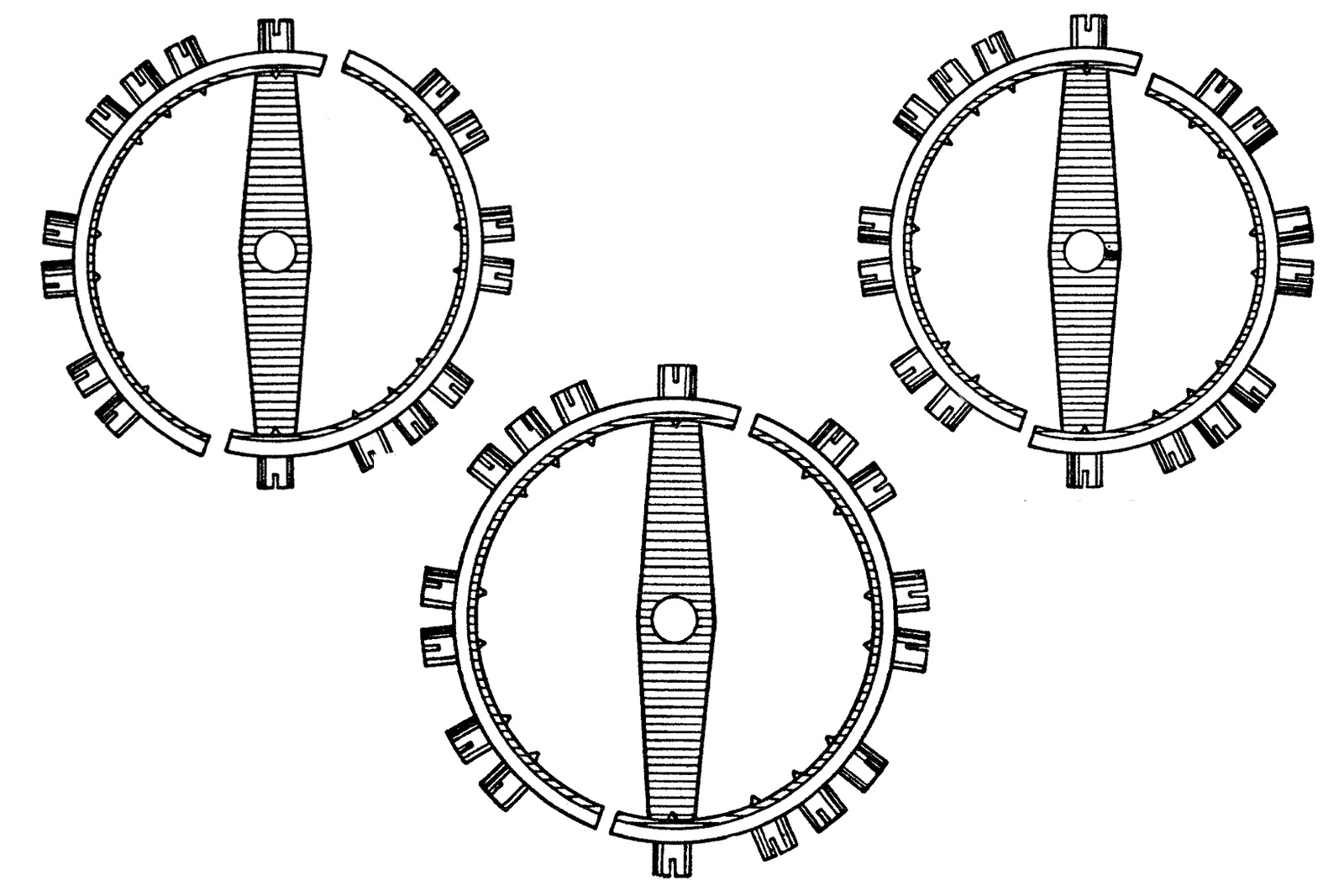
This is how the bi-metallic compensation balances came to be. Pierre Le Roy (1717 -1785) invented the first bi-metallic compensation balances. Arnold, Thomas Earnshaw (1749-1829) and Ferdinand Berthoud (1727-1807) later made contributions to the concept.

The basic construction of a bi-metallic balance features cut compensation arms made of an inner layer of steel and a thicker, outer layer of brass. Screws or weights would be typically fitted to these arms, much like in modern balances. 

The device would slightly curve inwards or outwards at different  temperatures, because brass and steel have different linear temperature expansion coefficients (α) and their expansion was not even. 

At low temperatures, the brass strip contracts faster than the steel inner layer, causing the curves to move outward. This would in turn increases the moment of inertia of the balance and slow down the stiffened balance. At high temperatures the opposite was the case, with the brass expanding fast and turning the curves inward, decreasing the moment of inertia. This would speed up the weakened balance. The short animation below provides a dynamic explanation of how the device works. At first sight, the system seemed foolproof.

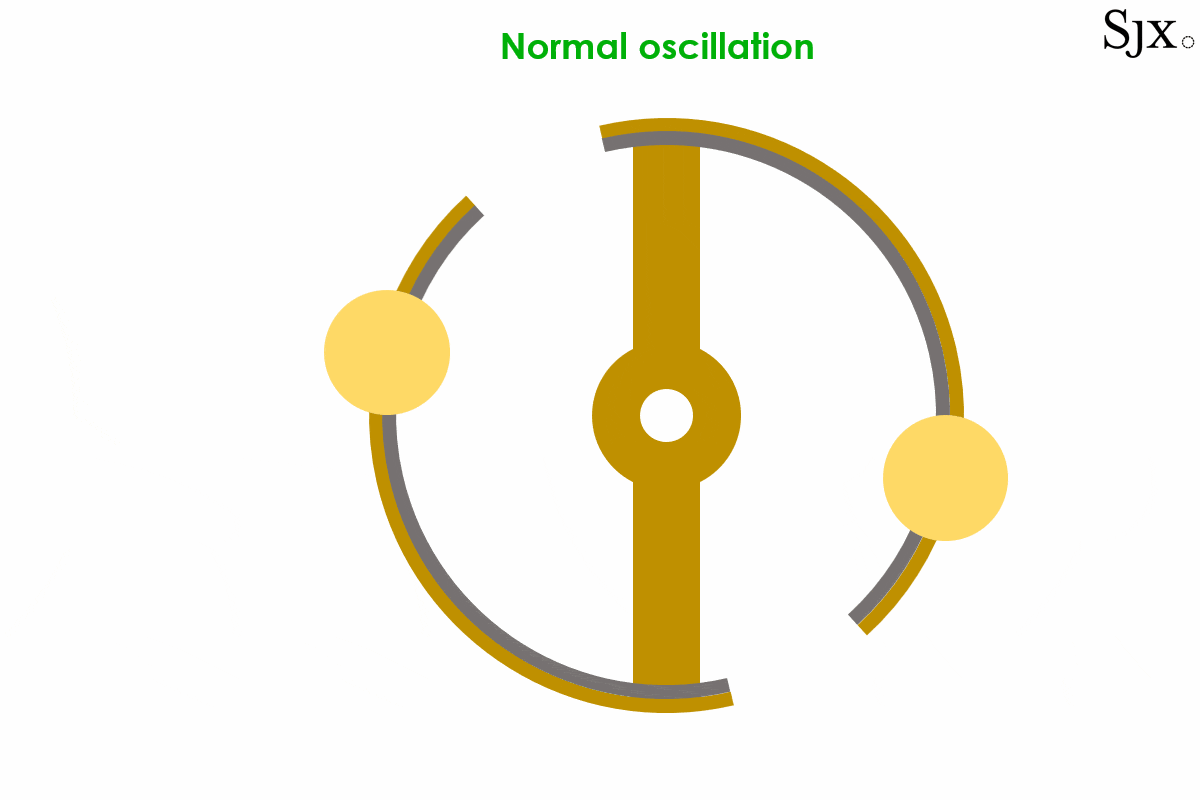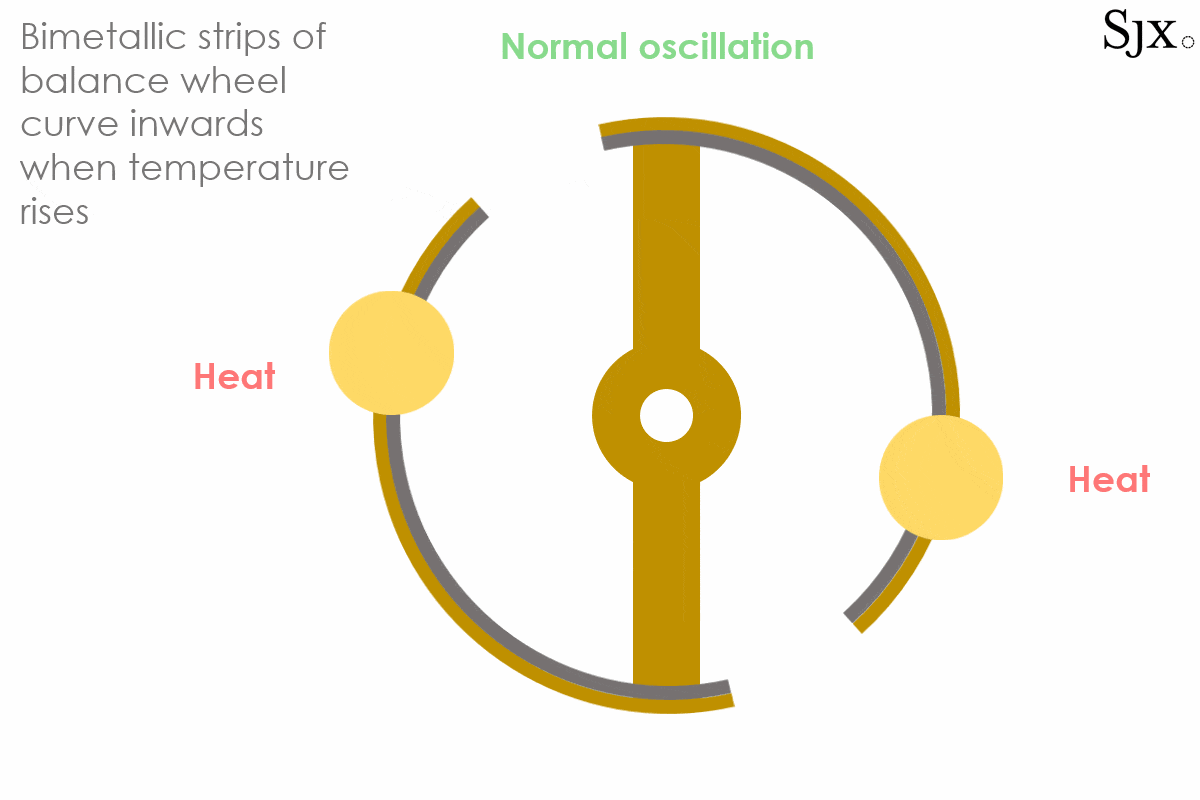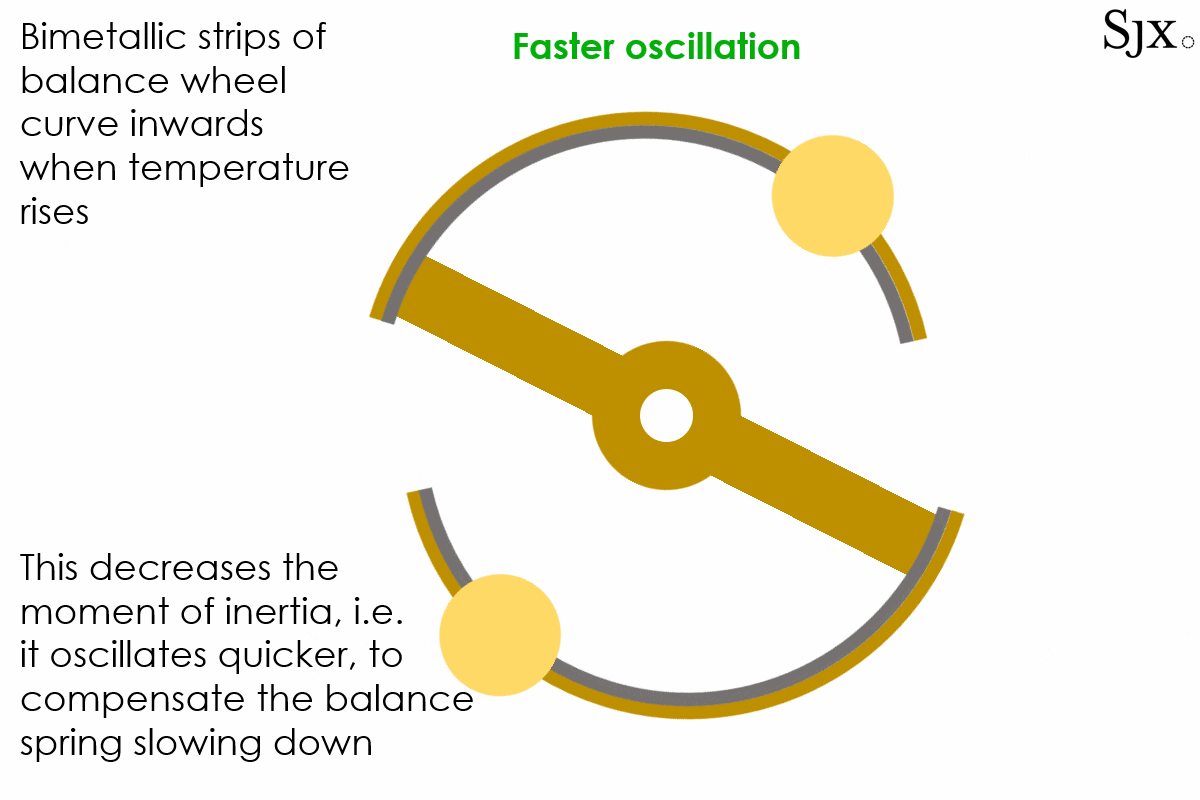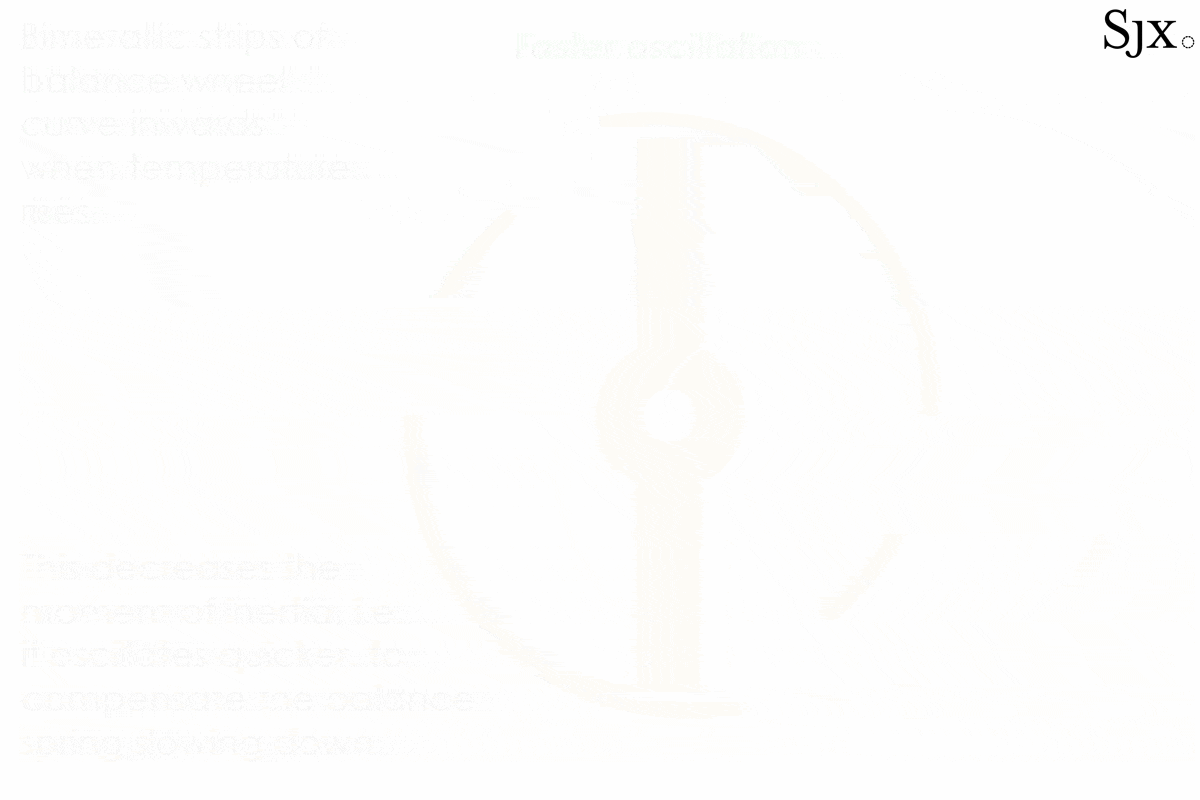
The oscillation of a bi-metallic balance wheel.

After thorough experimentation, especially with precise marine chronometers, watchmakers discovered an abnormality with the compensation mechanism. While the system worked well when set at the lower and higher bounds of the temperature spectrum (usually 0°C and 30°C respectively), the balance would not compensate well for the intermediate temperature values. 

The effect was dubbed the middle temperature error (MLE), also known secondary error. The discovery of this phenomenon is commonly attributed to Ferdinand Berthoud in 1771. 

Having discovered the MLE, watchmakers were left wondering about what was the cause. One of the first explanations that held for a while was related to the mathematical expression of the balance frequency, where the polar moment variation would be linear while the spring stiffness change would be under a square root — so their ratio would not hold constant. 

The explanation was true in part, but insufficient. There was an underlying cause behind the MLE, but one which escaped watchmakers. That matter was finally solved and corrected in the latter half of the 19th century, by a Swiss physicist who then went on to win a Nobel prize.

The Guillaume balance

Charles Édouard Guillaume (1861-2938) was born to Swiss parents in Fleurier, Switzerland. His father was a watchmaker and the young Guillaume showed interest in marine chronometry. He took a different path from his father however, and pursued experimental physics, eventually earning a PhD in 1883 from ETH Zurich, one of Europe’s most prestigious technical universities.

He later headed the International Bureau of Weights and Measures, where he carried on with his personal research and experiments. After the metric system was adopted, the Bureau occupied themselves with building metre-long rulers made from a suitable material that would be as impervious to atmospheric changes as possible (heat and humidity).

A platinum-iridium alloy behaved the best, but the material was expensive. The bureau was in search of a cheaper alloy, but with similar qualities. This is when sample ingots of iron-nickel alloys came by Guillaume’s desk.  

Even before studying Invar alloys, Guillaume was preoccupied with the underlying reason behind the MLE defect. He eventually found the subtle effect that caused the abnormal behaviour. The steel-brass balance would vary its shape quasi-linearly in relation to temperature, while there was a curve in the spring’s stiffness change. The figure below explains it better. 

The dark yellow line shows how the brass expansion affects the running rate. The green line shows how the steel alone affects the running of the balance. Their joint action is shown by the straight line in grey. By coincidence, the quadratic coefficients (beta) of brass and steel are sensibly the same, so they cancel out for the bi-metallic balance. This is why the dependence between temperature and rate change for such a balance is linear.

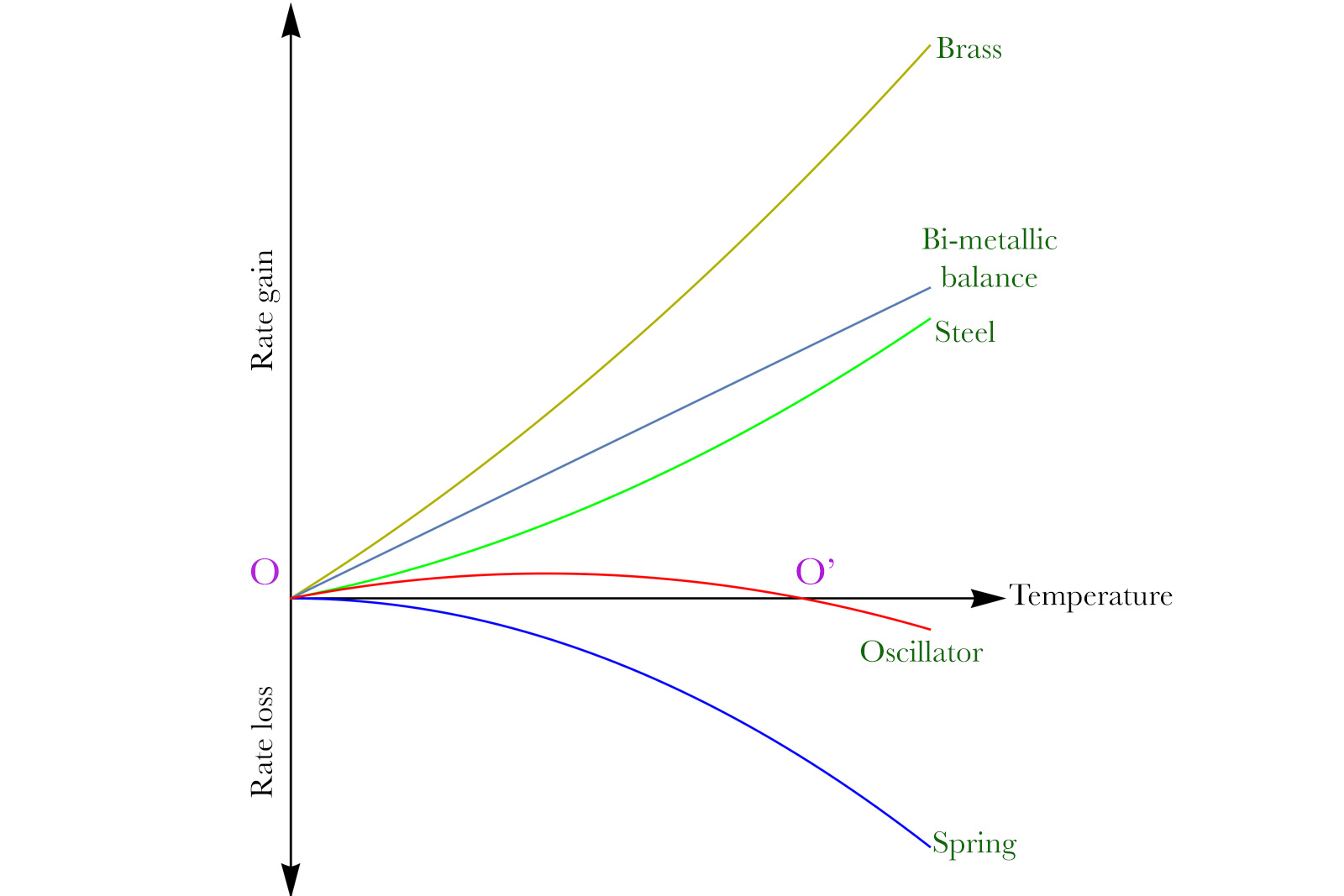
Figure adapted from Guillaume’s Nobel Prize lecture.

The blue downward slope shows the slowing effect of the hairspring as the temperature rises. Since the balance behaves linearly while the spring clearly does not, their respective effects can’t fully cancel out. The red line shows the compensated oscillator, an algebraic sum of the bi-metallic balance and spring effects. It is clear that such an oscillator’s rate remains dependent on the temperature. 

There are only two points O and O’ where the red slope intersects the horizontal axis — thus pointing to a zero rate change. Those points are usually the lower and upper bounds of temperature regulation, where the watch runs perfectly. The intermediate temperatures however lead to a slight but noticeable rate gain of 3-4 seconds per day.

Invar

As mentioned before, Guillaume came by steel-nickel alloys during his tenure at the International Bureau of Weights and Measures. He noticed an anomaly in the heat expansion behaviour of those alloys. For most two-metal alloys, the dilatation coefficient (α) sits somewhere between the respective expansion coefficients of the pure metal constituents. It was initially expected that a iron-nickel alloy would behave in a similar fashion.

What Guillaume observed was a seemingly erratic behaviour, with an expansion coefficient α that followed an odd curve which reached its minimum at a composition of 36% nickel. At that specific point, the linear expansion coefficient is 10 to 11 times smaller than that of steel. 

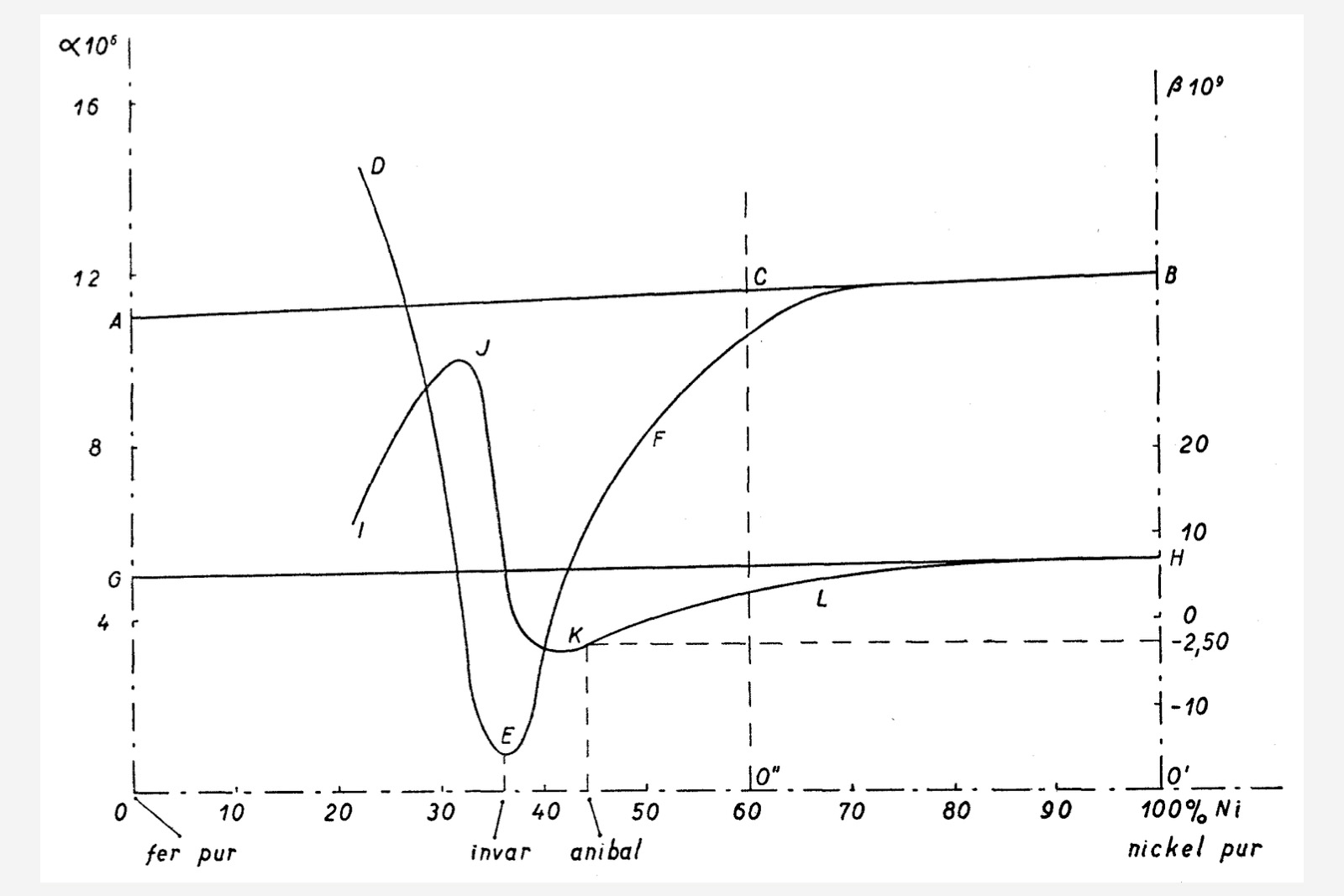
Diagram extracted from L. Defossez, Théorie générale de l’horlogerie Tome II,  showing the odd curves for the α and β coefficients in iron-nickel alloys; α’s variance with composition is shown by curve DEFG, while β’s is shown by curve IJKL

The quadratic coefficient β follows its own non-linear curve as well and has negative values for alloys with nickel concentrations of at least 36-37%. This subtracts from the already small linear expansion coefficient, making for a quasi-null temperature-related global change in dimensions. From this convenient invariability in size in relation to temperature change, Guillaume coined the term Invar for this interesting family of alloys.

Invar was famously used to replace the inner steel strip in bi-metallic balances. Since Invar expands different from steel, the compensation action of the cut balance wasn’t linear anymore, but followed its own curve. By 1899 Guillaume calculated the advantageous Invar alloy composition (about 44% nickel) which would cancel out the spring effect completely. Still part of the Invar family of alloys, this specific composition was referred to as Anibal.

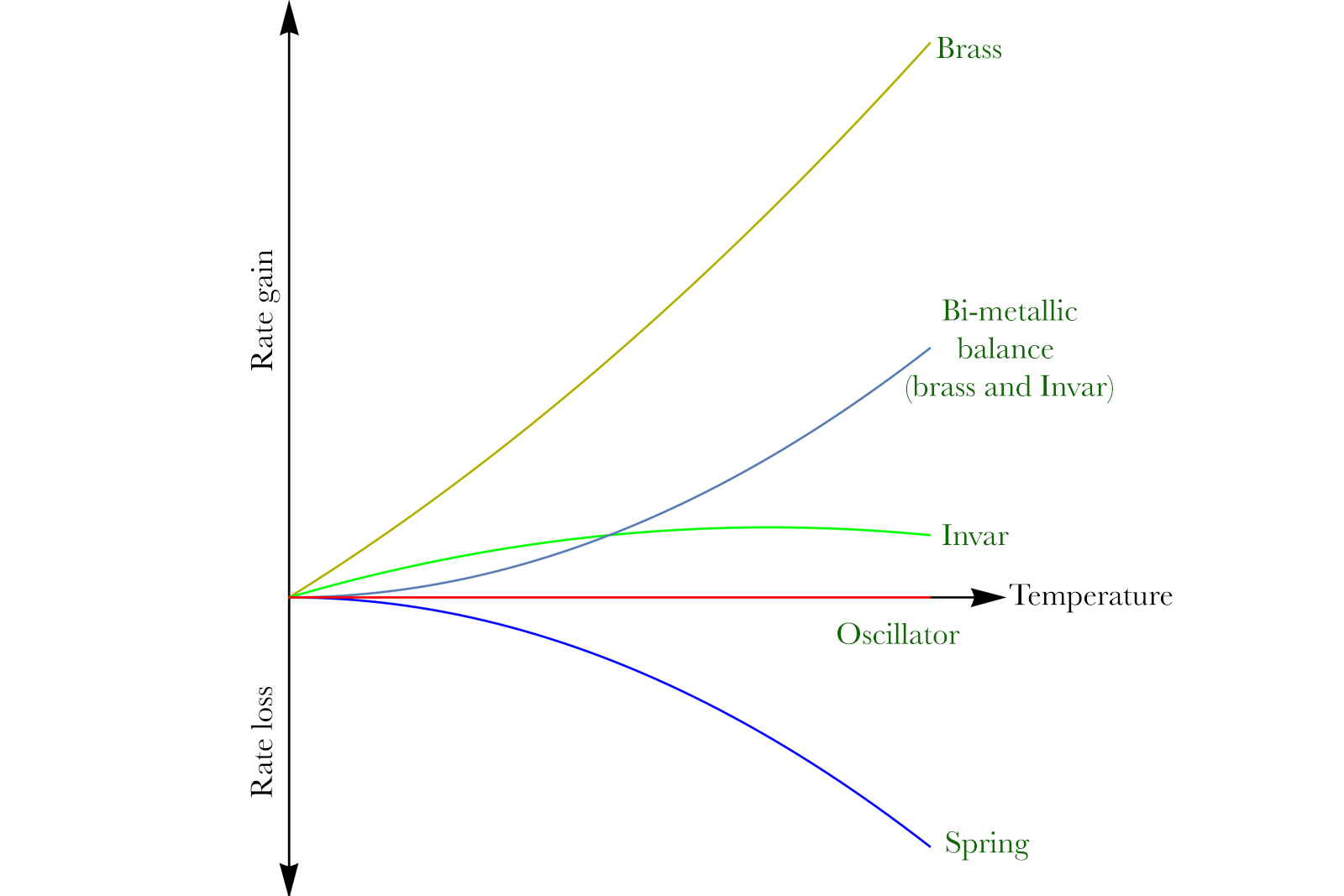
Figure adapted from Guillaume’s Nobel Prize lecture.

The figure below shows how that works. The green line shows the Invar strip’s influence, which has a very different profile from that of steel. The grey line shows how the new brass-Invar balance affects the rate of the watch as temperature rises. Its curve is quasi-identical in profile to the spring’s (blue), but opposite in sign — so their sum is zero for all temperatures (flat red line for the oscillator). This became known as a Guillaume balance. 

Elinvar

A friend and collaborator of Guillaume’s, watchmaker Paul Perret (1854-1904) carried his own experiments with Invar alloys. The matter of compensation balances being settled, he sought to apply the wondrous alloy to the hairspring itself. When doing so, he noticed that the prototype springs would speed up as the temperature rose — a stark difference from all the other hairsprings in production. 

As shown in previous figures, as temperature increases, steel balance springs lead to a rate loss for the oscillator as they weaken. Perret was baffled to see the Invar springs do the exact opposite and transmitted his observations back to Guillaume. 

Perret’s experimentations led the physicist to conclude that iron-nickel alloys presented simultaneous expansion and thermoelastic anomalies. In 1912 Guillaume started adding chromium and manganese to the iron-nickel base, in order to concoct an alloy with a near-zero thermoelastic variance — an alloy that would keep its stiffness across a wide range of temperatures.  

By Adrien Jaquerod’s biography, Charles-Edouard Guillaume: 1861-1938, the physicist’s work with Invar alloys concluded in 1919. Then Guillaume presented the Elinvar spring — a contraction of élasticité invariable, or “invariable elasticity” in English. Originally consisting of 34% nickel (much as early Invar samples), 54% iron and the addition of 12% chromium, Elinvar was a true breakthrough for watchmakers, since it rendered the need for complicated compensation balances obsolete. Elinvar was believed to keep the same Young’s modulus from -50°C to +100°C.

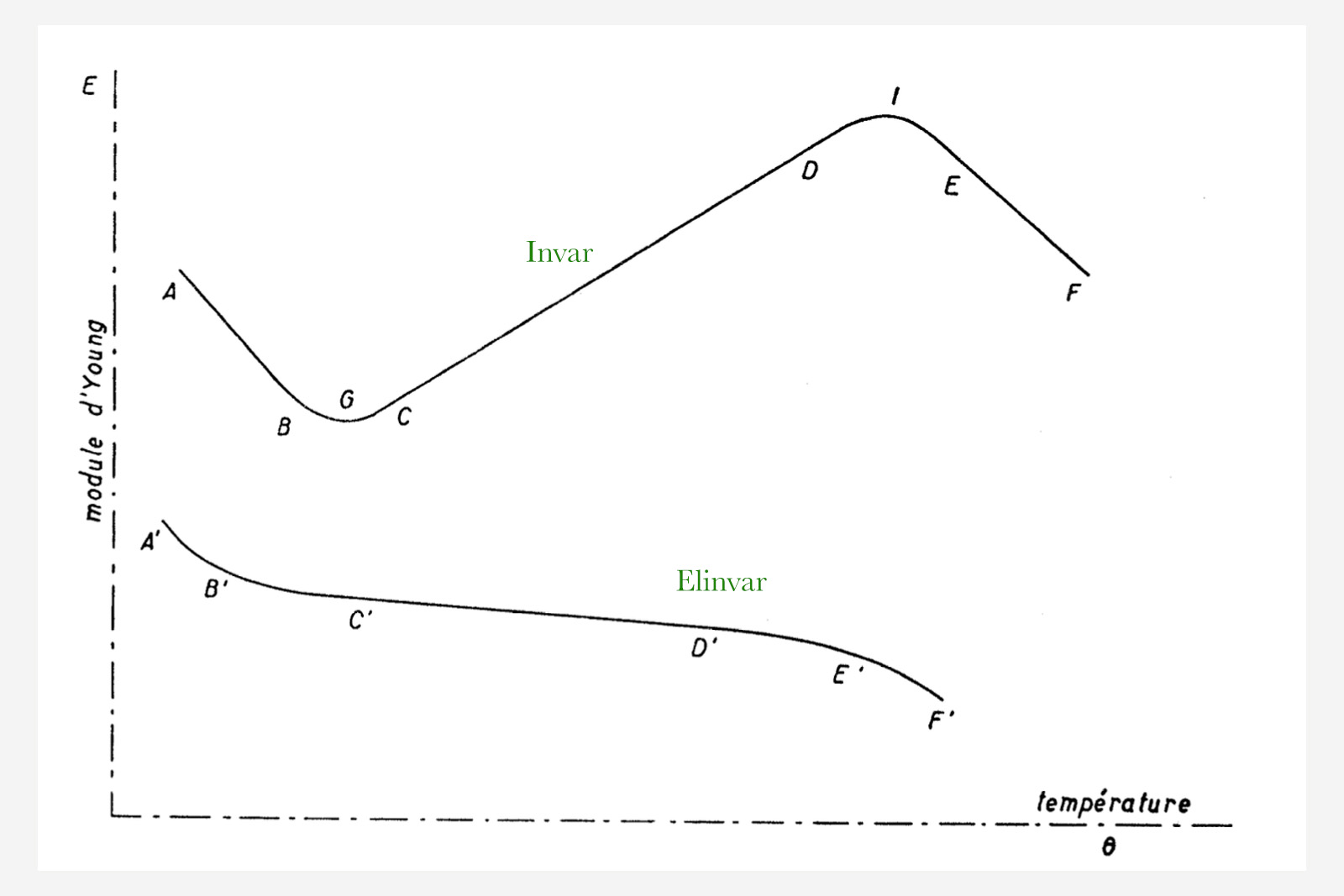
Figure extracted from L. Defossez, Théorie générale de l’horlogerie Tome II, showing the little variance of Elinvar’s Young’s modulus with temperature; on the segment C’D’ the change is almost null.

The introduction of Elinvar springs, which were malleable, corrosion resistant and even resistant to magnetic influence to a degree, changed the watchmaking industry. This ushered the new era of monometallic balances and mass-produced accurate timekeepers.

In 1920 Guillaume was awarded the Nobel Prize in Physics in recognition of his discovery of anomalies in iron-nickel alloys. His work proved very important to all sorts of engineering branches beyond horology. From structural engineering to diverse scientific instruments (seismographs of the time for example) and light bulbs, the discovery of Invar alloys proved to be one of the quieter but very important breakthroughs of the late 19th century. 

As a short aside of why Invar and its derivates seem impervious to temperature-induced changes, the answer is linked to its particular molecular behaviour. Iron-nickel alloys exhibit what is known as a magnetostriction effect — not present in neither pure iron nor pure nickel. A simple explanation is provided by M. F. Ashby et al. in the textbook Materials: Engineering science, processing and design.

Normal materials exhibit an increased atomic vibration when heat is added to them. This vibrations expands the lattice, effectively increasing the volume of said material. For iron-nickel alloys, the iron atoms in the lattice also have their own inherent magnetic moments. When the temperature rises, the magnetostriction causes the iron atoms to tighten together due to magnetic transition. 

In fact, the two events happen simultaneously and cancel each other (when the iron-nickel ratio is favourable) — thus leading to a quasi-null volume increase. The addition of “quasi-” was used throughout this story since a true canceling out of the opposing effects described rarely occurs, even though the residual errors are close to negligible.

Looking forward

The introduction of Elinvar was considered at the time the ultimate hairspring material and was widely adopted by watchmakers across the world. It was used it the last of marine chronometers and found its way to consumer pocket and eventually wrist-worn watches.

Elinvar was quickly adopted by both artisans and industrial manufacturers alike and remained the de facto hairspring material for a long while. George Daniels and Derek Pratt famously liked new old-stock Hamilton 22 caliber hairsprings made from Elinvar, which they hailed as the best ever produced. Currently active American watchmaker David Walter favours them as well, which speaks on how well Elinvar performs.

While Elinvar finally solved the issue of temperature-related rate change, a new disruptive factor became increasingly problematic: magnetism. As electrical networks and devices became more and more prevalent in our lives so did magnetic fields.

As mentioned, Elinvar has a limited non-magnetic quality, but it becomes magnetised by strong enough fields — which are now household occurrences: computers, speakers, various appliances. The wondrous hairspring slowly became insufficient, pushing a new generation of watchmakers and engineers to search for improved alloys.