While the invention of the spiral hairspring by Christiaan Huygens in 1675 kickstarted a revolution in terms of portable precision timekeeping, the concept was far from fully developed. It was arguably only with the later invention of the overcoil hairspring that the ideal oscillator in portable watches emerged.

For many years horologists — theoreticians and artisans alike — worked to perfect the balance-hairspring assembly to optimise its performance, notably in terms of isochronism. True isochronism became a sort of holy grail for watchmakers all around the world, who all sought to ameliorate the inherent quirks of the sprung oscillator.

The recent Breguet Soucription features an overcoil hairspring of non-magnetic Nivachron alloy

The need for end curves

The quest for isochronism was a true challenge for horologists. Isochronism is the ability of the balance-hairspring assembly the have the same period of oscillation for small and large amplitudes alike. In other words, the balance oscillation takes the same period of time regardless of the degree travelled.

This is very important, since a balance usually swings with high amplitude with a fully wound mainspring and then runs at progressively smaller amplitude as the barrel unwinds. As a timepiece is required to keep good time regardless of  its winding state, an oscillator whose period is independent from its amplitude is needed. (Another solution to this is to optimise the energy delivery from the mainspring with a constant force mechanism, which is another topic entirely.)

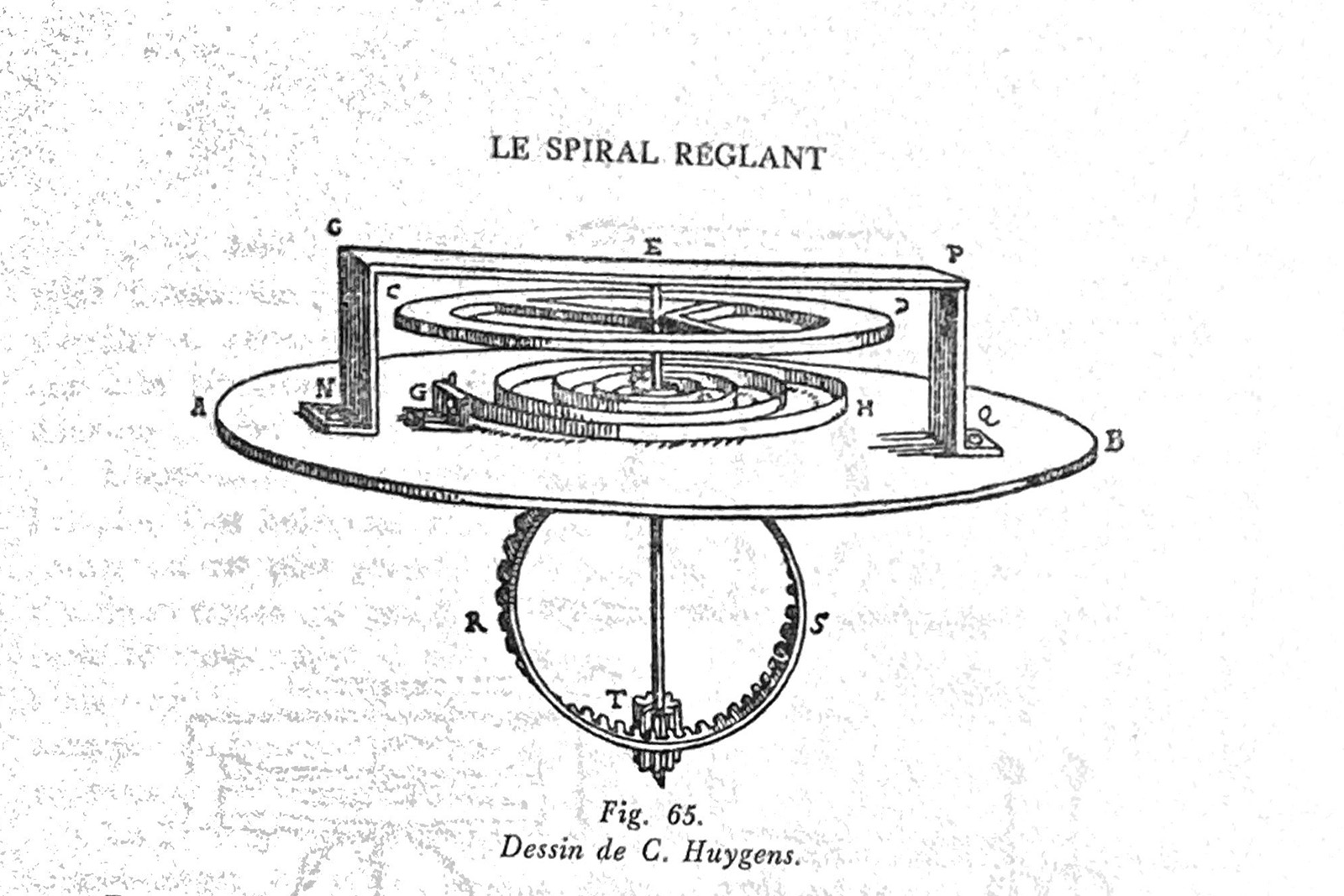
Huygens’ drawing of an early hairspring embodiment

The balance-hairspring model is theoretically isochronous — but only on paper with ideal conditions assumed. In practice friction and slight equilibrium defects can disrupt the oscillator’s ideal running, making the timepiece’s accuracy dependent on the state of winding. 

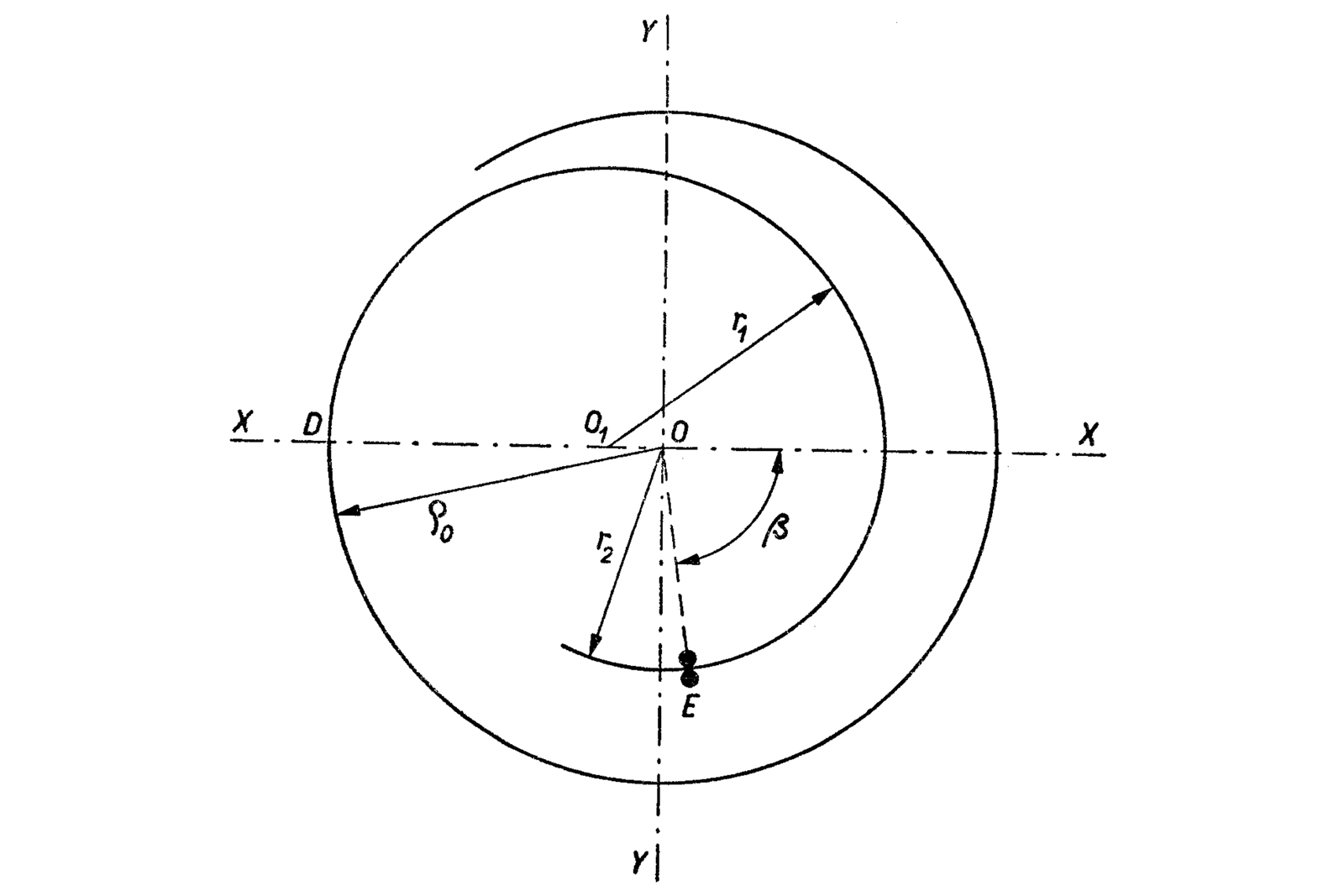
A large issue that was noticed early by watchmakers was the uneven development of the hairspring. This happens due to a geometrical constraint of the system, with the fixed outer pinning point not allowing the hairspring to “breathe” concentrically. We explained this a little more in our piece on the Ulysse Nardin Freak and the development of the silicon hairspring. 

The uneven development of the hairspring harms the oscillator in two distinct ways: the eccentric movement of the coils displaces the spring’s center of gravity away from the balance’s axis, creating a disequilibrium and the uneven development strains the pivots because the coils apply unwanted side pressure to the axle. 

The displacement in the centre of gravity was found to be negligible, since it tends to virtually cancel out during two alternations — so the net centre of gravity vector displacement over one full oscillation is not really a concern. 

The torque directed onto the pivots however is the larger issue, since the pivots themselves distribute that force into their jewels, increasing friction and creating wear patterns in time. This pressure can’t be cancelled out and the generated friction force actively disrupts the oscillator’s isochronism.

A logical solution to this would be to force the hairspring to develop concentrically so that the residual couple applied to the inner pinning point — thus to the pivots — would be as close to zero as possible. This is where end curves come into play.

An overcool in the Lange Zeitwerk L043.3

A short history of end curves

As early as the 17th century a French watchmaker by the name of Gourdain used a sort of courbes tâtées  — literally “touched” (or more accurately, “corrected”) curves. Empirically formed by the artisan, these curves seemed to improve the balance spring’s “breathing”.

A great breakthrough later came from John Arnold (1736-1799) who shaped the ends of his cylindrical hairsprings into sharp inward curves connecting the spring ends to the balance collet and the upper bridge pinning point respectively. 

Modern cylindrical hairspring in a Moser tourbillon

Abraham-Louis Breguet (1747-1823), a friend of Arnold’s, borrowed from his work and adapted the Englishman’s end curves to flat balance springs — giving birth to the Breguet overcoil. The talented watchmaker noticed that raising the last coil of the hairspring into a plane parallel to the other coils and curving it slightly towards the outer pinning point made the spring “breathe” concentrically. 

Edouard Phillips

These early overcoils were empirically shaped by watchmakers, who adjusted and bent the curve as they saw fit after observing how the timepiece performed over a period of time. There was no rigorous theory involved in forming the end curves and watchmakers didn’t have a definitive explanation for how and why the method worked. 

This is where the French engineer and mathematician Edouard Phillips (1821-1889) stepped in and assembled a rigorous mathematical theory of end curves — which still stands as a reference today. 

By trade Phillips was a “mine engineer” who focused on material and structure sciences. He developed his own theories on blade springs of different geometries and the torques they could provide. During his lifetime he was chair of mechanics at the prestigious École Polytechnique and a member of the Académie des sciences. 

During the latter part of his life, Phillips dedicated himself to the study of horology, more precisely to the study of the hairspring — a particular embodiment of a blade spring, after all. In 1860 he published a groundbreaking paper, Mémoire sur le spiral réglant des chronomètres et des montres, where he studied the behaviour of an end curve. Phillips concludes by giving some rules for shaping an ideal hairspring, which are now known as “Phillips conditions”. 

Extract from E. Phillips’ “Mémoire sur le spiral réglant des chronomètres et des montres”

The outer end curve

In his paper Phillips started out by assuming the uneven development of coils exerts some torque on the pivots. Then he started out mathematically exploring what would cancel out that unwanted torque. 

Through a lengthly process involving integral calculus, he applied his own theories of elasticity to the hairspring model and came up with a method of keeping the spring’s coils centred on the balance’s axis. The conditions he found gave birth to the Phillips end curve — a perfected overcoil which reduces the lateral pivot pressure to the point of virtually canceling it out.

The Phillips conditions for overcoils can be summed up in a few words and a short mathematical expression:

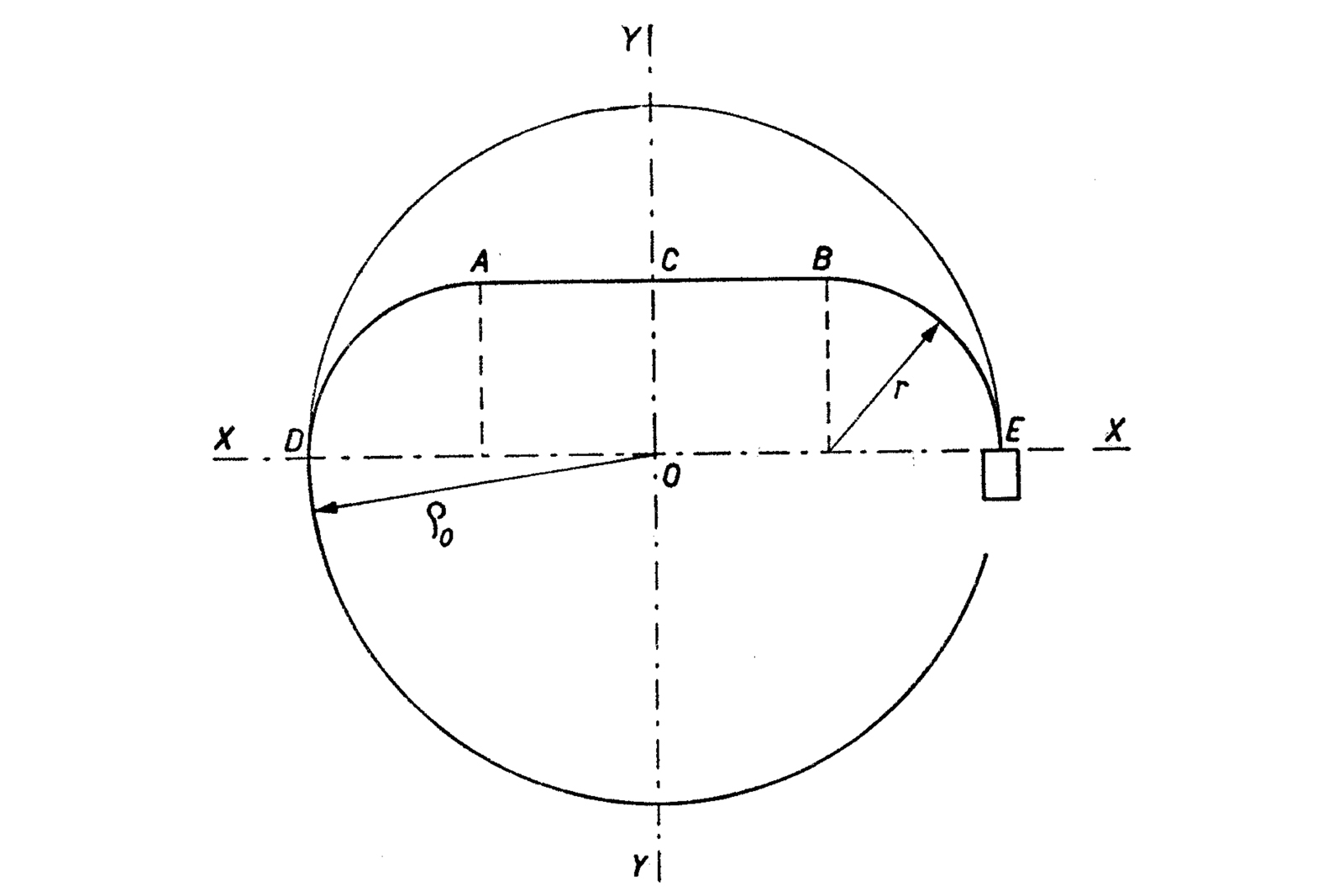
The centre of gravity of the terminal curve has to be placed on a radius perpendicular to the line joining the spiral’s centre of gravity and the point where the curve breaks off from the spiral. The distance of the curve’s centre of gravity to the spiral’s centre of gravity needs to be equal to the spiral’s radius squared, divided by the length of the end curve. 

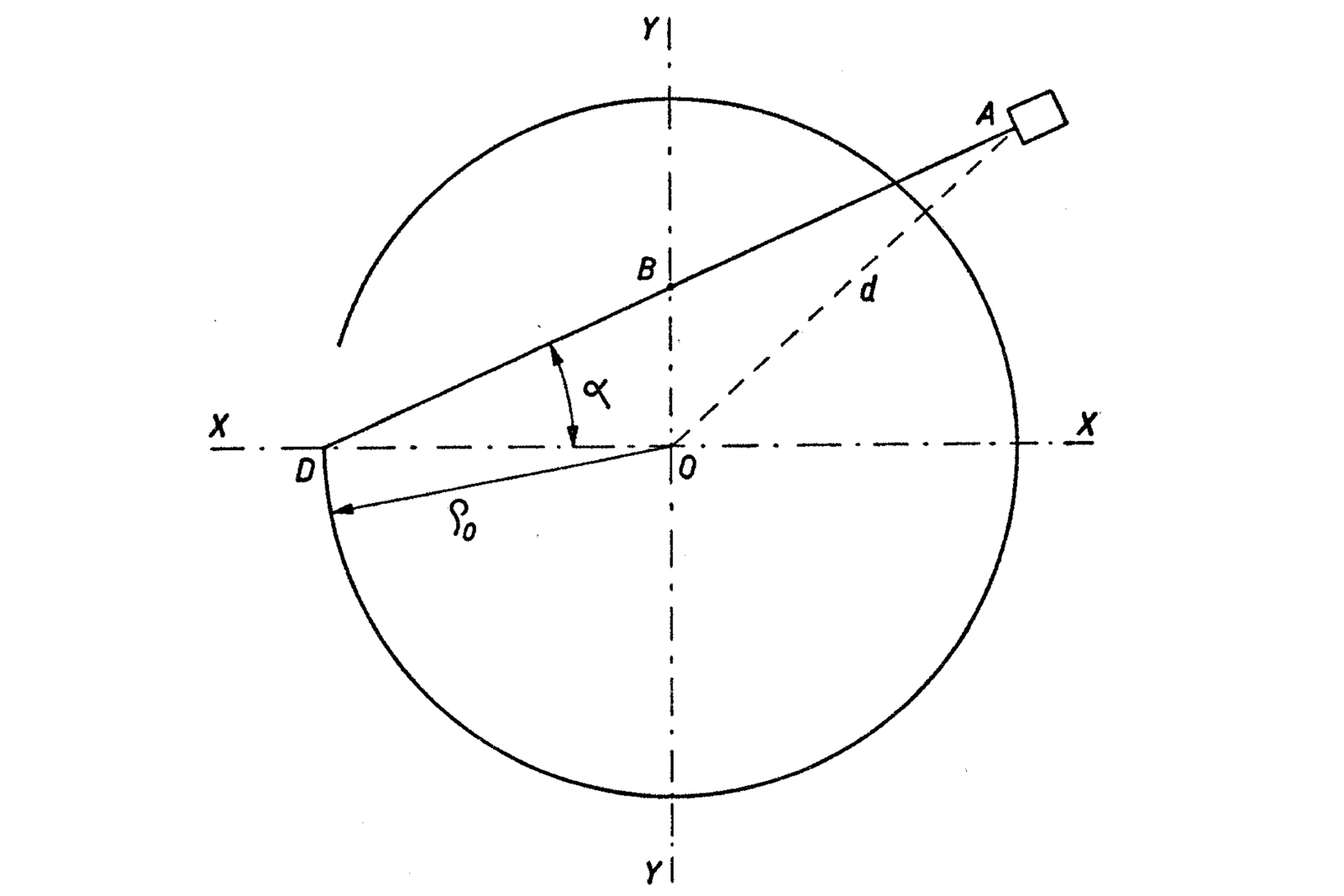
The concept might seem complicated but is straightforward enough to implement in real hairsprings. The figure below may be more suggestive for grasping the proportions. The starting point of the overcoil A is coincident with axis Ox. The gravity centre G of the end curve sits perpendicular to that axis, on Oy.

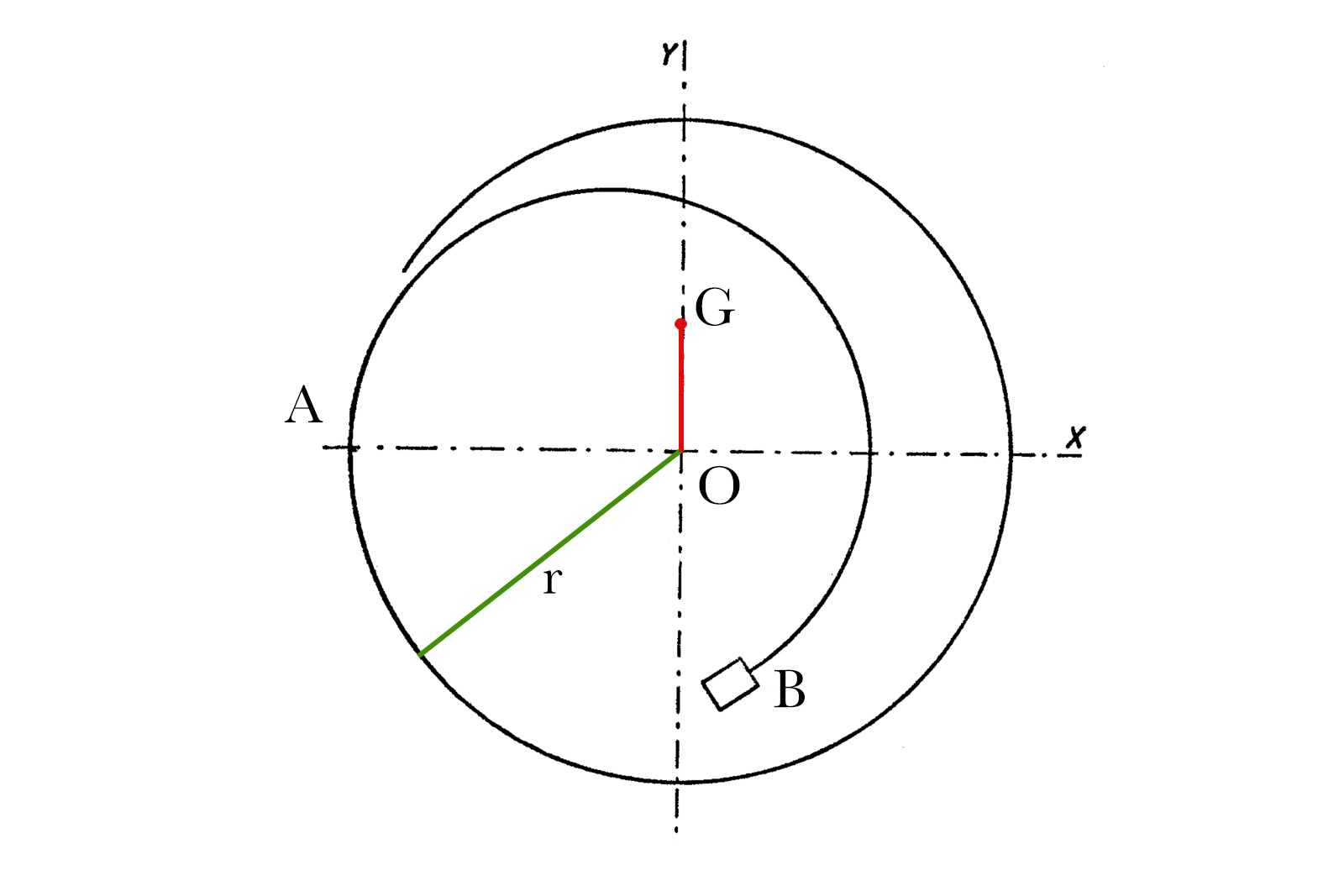
Interestingly, Phillips’ condition doesn’t mandate any sort of particular geometry of the overcoil; as long as the equation is satisfied the end curve can take on any shape. This explains why different brands and watchmakers use slightly different overcoil geometries. Phillips also noticed that the overcoils were more effective for larger hairsprings. 

Common shapes of overcoils

One of the simplest types of overcoils (which satisfies Phillips’ equation) is the circle arc end curve. The plain shape breaks off from the spiral and arches towards the pinning point. The curve is uniform and circular while the arc it describes is fairly short. Below is figure by L. Defossez, detailing the particular geometry of such a curve. 

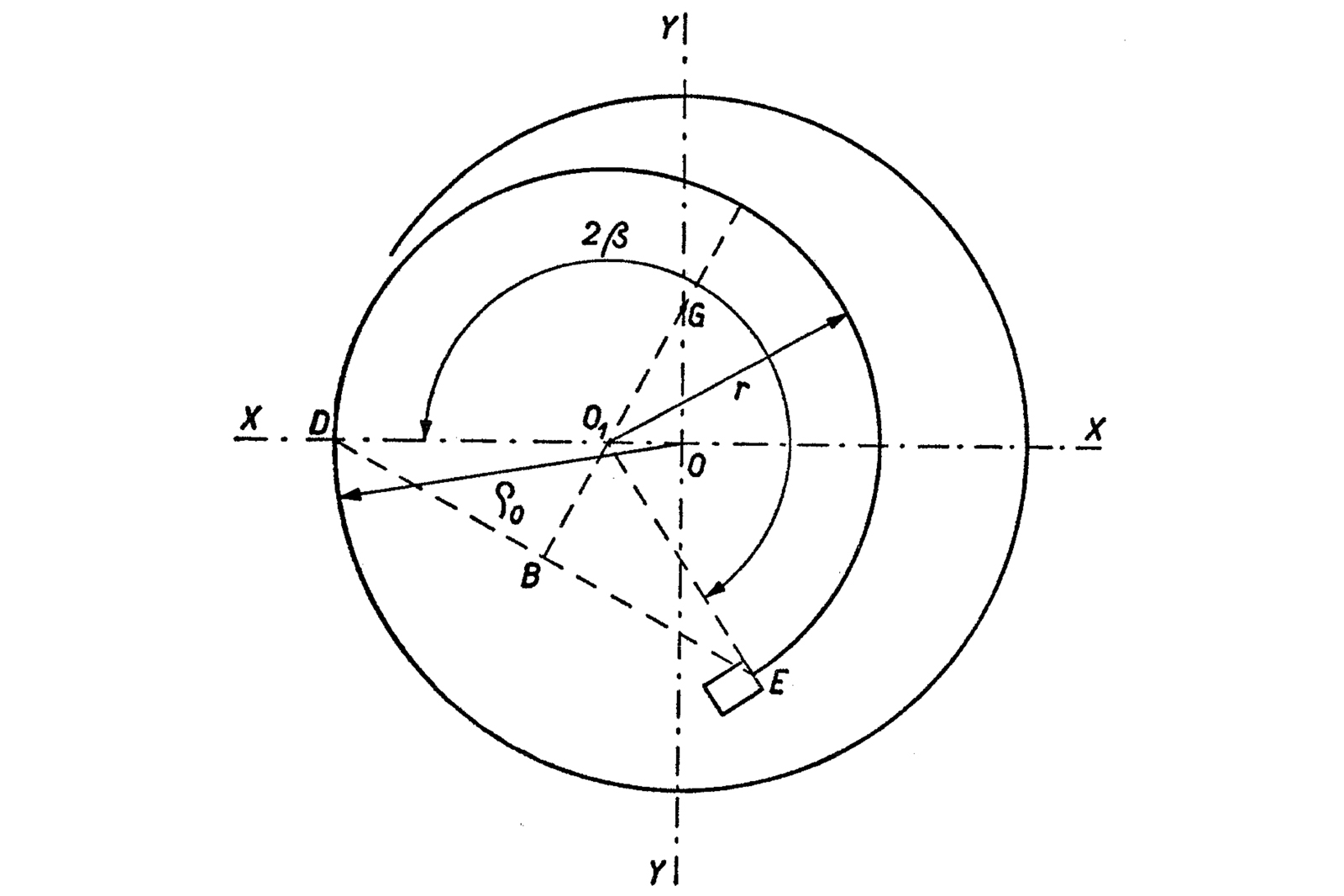
Overcoil made of one circle arc. Image – L. Defossez

Other overcoils are made of two circle arcs of different radiuses, giving the final curve an elongated shape. Some movements with a spring regulator use this geometry, as the second arc’s centre coincides with the spring’s centre and a traditional raquette can be employed.

Overcoil made of two circe arcs with different radiuses. Image – L. Defossez

An early 20th century Patek Philippe pocket watch movement with a classic high-end chronometer hairspring set up

Today most brands use a simpler geometry, that of two circle arcs linked by a straight segment. Compared to the purely circular end curve, this shape is easier to bend. Variations of this geometry can be seen in industrially manufactured movements from the likes of Rolex or IWC. 

Overcoil model with two circle arcs joined by a segment. Image – L. Defossez

The MB&F LM QP movement sports a very prominent overcoil

Straight terminal curve which satisfies Phillips’ condition. While theoretically sound, such an overcoil was never used to the author’s knowledge. Image – L. Defossez

The inner (or Grossmann) curve

Edouard Phillips based his studies on helical springs, which would feature two symmetrical curves, one joining the outer pinning point and the other the inner pinning point. This model does not fit entirely with flat springs, which have different diameters for their outer and inner ends. 

Voutilainen tourbillon movement with a hairspring featuring an inner Grossmann curve.

While overcoils may counteract most of the uneven development of the hairspring, reducing the side pressure on the pivot, some argue the innermost coils of the spiral have their own destructive effect as they unwind against the collet. 

The collet is the piece which joins the hairspring with the balance staff. Of circular shape, the collet has its own interactions with the inner coils of the hairsprings, which can exert some side pressures that the overcoil can’t cancel out. 

Jules Grossmann, a respected regleur from Le Locle, found Phillips’ discoveries consistent with his own extensive experience and observations adjusting overcoils. While he recognised the utility of calculus, he could not truly comprehend nor entirely follow Phillips’ methods. The subject stated with him nevertheless. 

Even in chronometers using theoretically perfect overcoils, Grossmann still noticed some running differences between horizontal positions — issue which he addressed by enunciating a set of attach point rules. These rules concern how many full turns a hairspring has and where the inner pinning point sits, relative to the outer pinning point. 

Grossmann also learnt at some point calculus all by himself, using available courses and books on the subject. Using his newly-acquired knowledge, Grossmann adapted Phillips’ theory on the inner end of flat hairsprings, creating the inner — or Grossmann — curve. This adjustment of the inner spiral seeks to cancel out any side pressure from the innermost coils of the hairspring.

Edouard Phillips eventually payed a visit to Jules Grossmann in Le Locle in 1871. The two horologists remained in contact until Phillips’ death in 1889. In his latter years Grossmann wrote an extensive, 450-page volume about precision watch regulation, Théorie du reglage. 

The practical utility of the inner curve is still debatable. George Daniels suggests in Watchmaking that “due to the difficulty of forming so small a curve accurately the results are uncertain”. He is indeed right, as Grossmann inner curves are very difficult to execute, requiring the hand of a highly skilled watchmaker.

Hairspring with both an outer Phillips overcoil and inner Grossmann curve. Image – L. Defossez

Inner curves are a rare find, with Voutilainen being one (if not the only) watchmaker to employ Grossmann curves consistently across his movements. The Vingt-8 series of calibers comes with a large balance, complete with a hairspring with both a Phillips overcoil and Grossmann inner curve. 

Makers using silicon hairsprings also seem to implement a kind of inner curve, which is easy to obtain with an etching process that can accommodate any kind of planar geometry. 

The Voutilainen Vingt-8 balance

Conclusions

The subject of overcoils and terminal curves remains a quite a fascinating topic for horologists. While the first solid theory of overcoils is over 160 years old, new technologies make way for novel end curve types which were inconceivable during Phillips’ time. De Bethune employs a proprietary hairspring, made of two separate pieces, one for the spiral and the other for the flat end coil. De Bethune claims the device performs as well as classic overcoils.

Manufacturers of silicon hairsprings have been employing specialised terminal curves since the beginning. While their approach is different from the likes of Edouard Phillips or Jules Grossmann, today’s engineers are experimenting with intricate geometries and new materials in crafting isochronous springs with little effort. The downside of these advancements is that traditional hand adjusting of end curves is becoming an increasingly rarer skill.